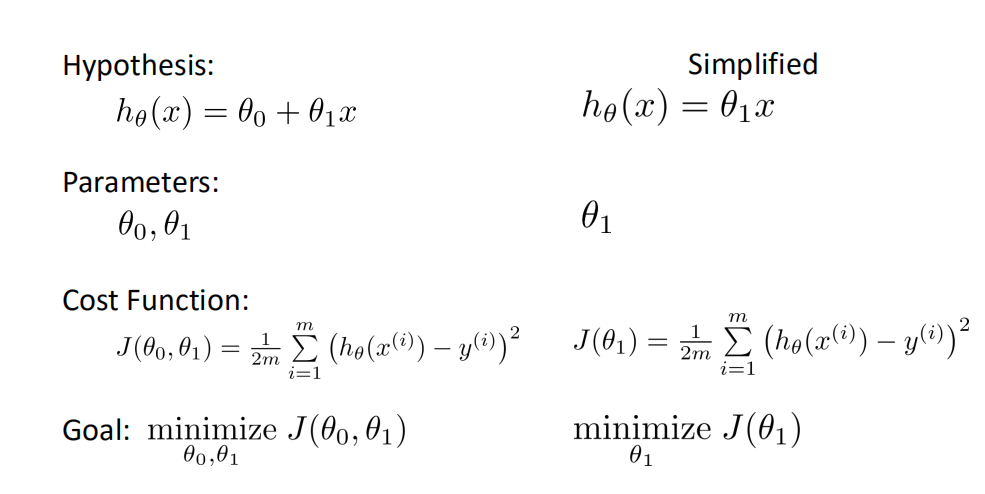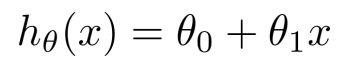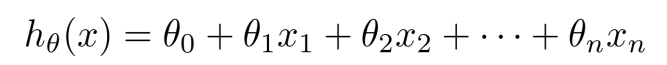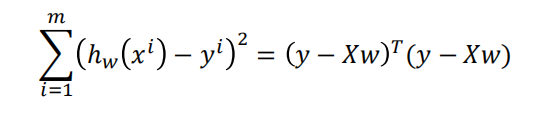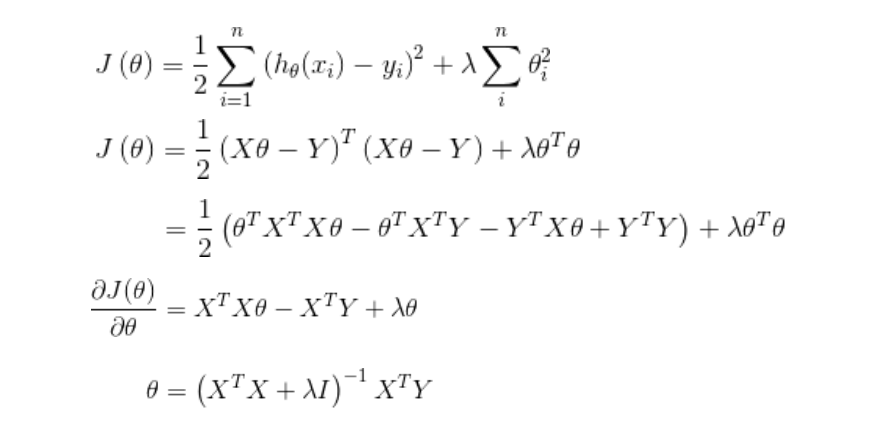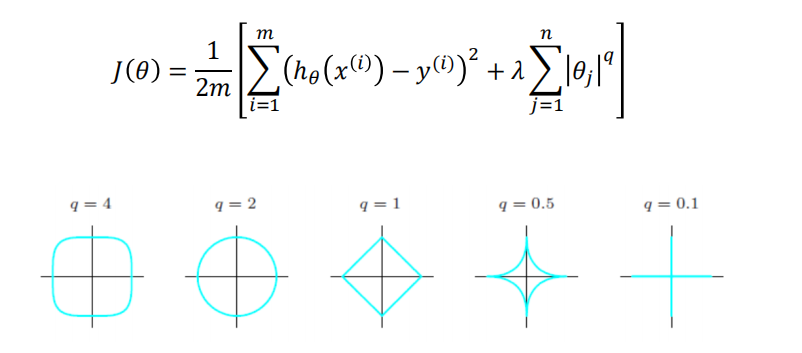线性回归与非线性回归

一直是阵雨🌦️ 收录于 machine learning

2020-03-06 约 4787 字预计阅读 10 分钟

基于梯度下降法的一元线性回归应用

回归Regression

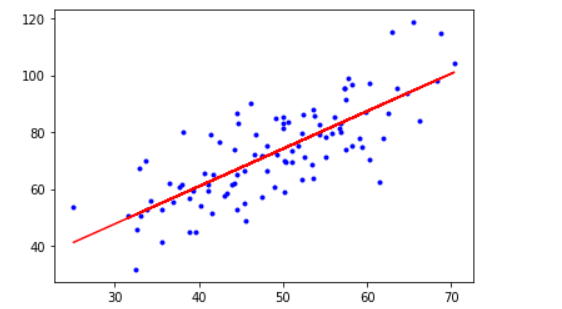
一元线性回归

回归分析(regression analysis)用来建立方程模拟两个或者多个变量之间如何关联
被预测的变量叫做：因变量(dependent variable), 输出(output)
被用来进行预测的变量叫做：自变量(independent variable), 输入(input)
一元线性回归包含一个自变量和一个因变量
以上两个变量的关系用一条直线来模拟
如果包含两个以上的自变量，则称作多元回归分析(multiple regression)

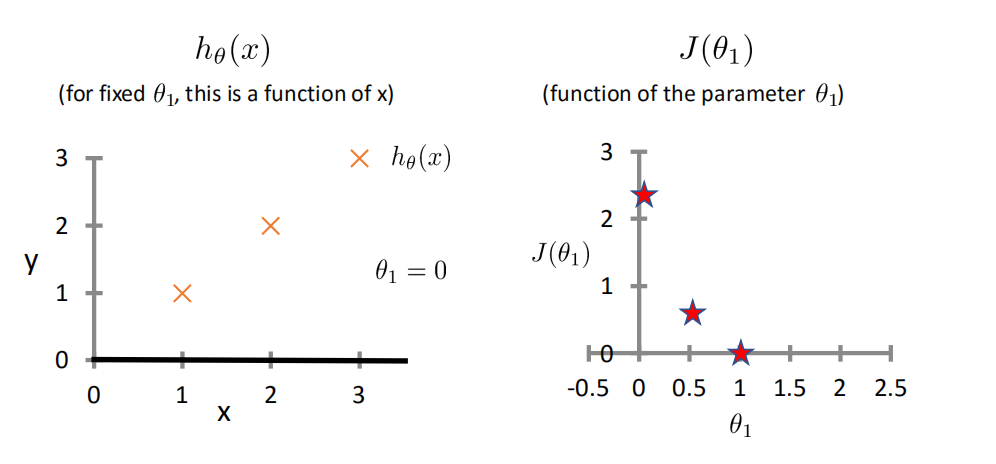
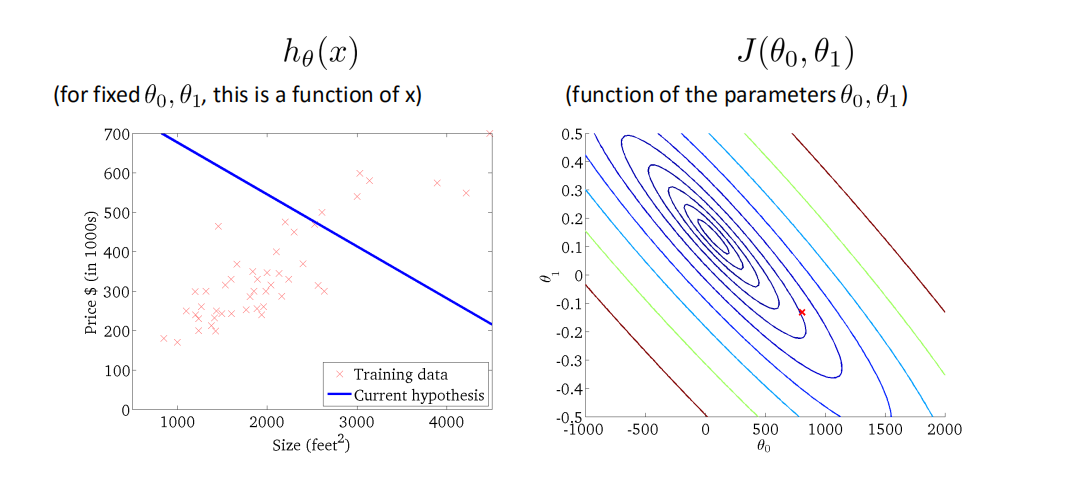
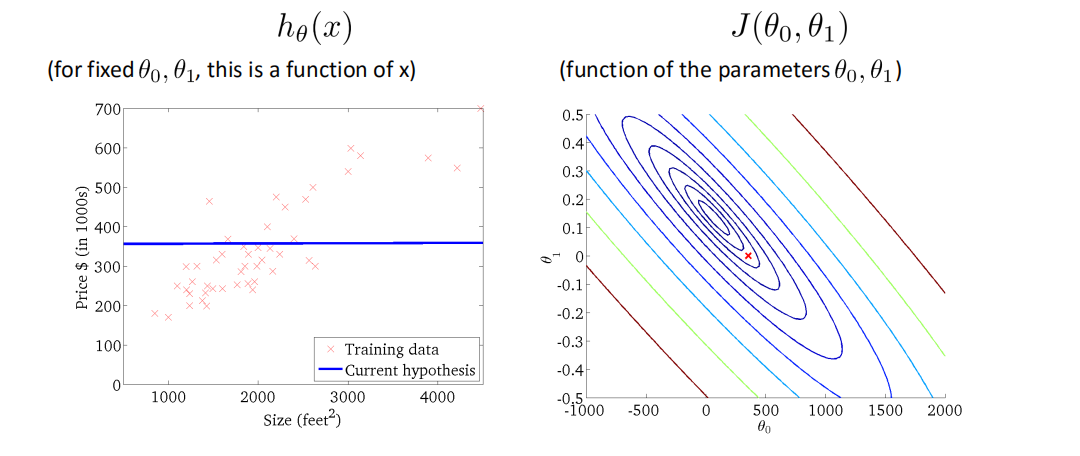
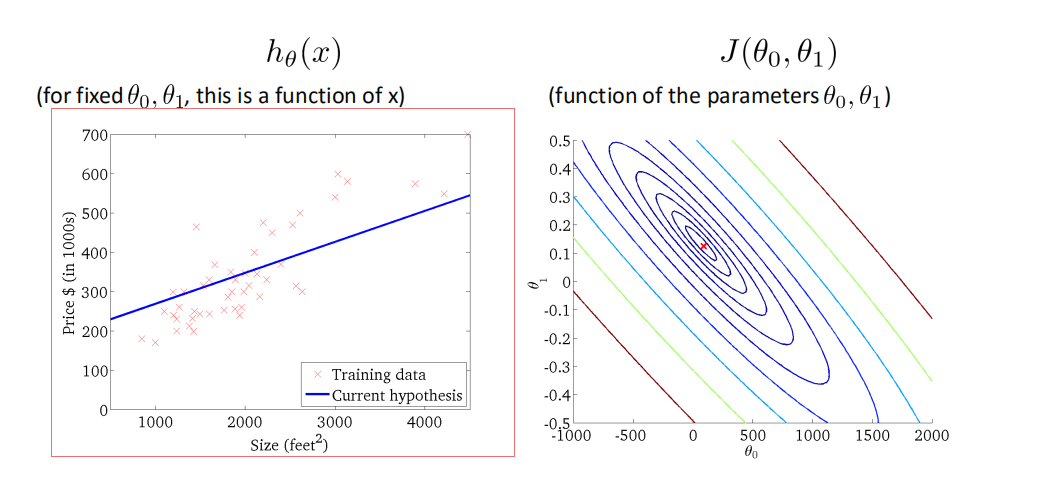
ℎ𝜃 𝑥 = 𝜃0 + 𝜃1𝑥

这个方程对应的图像是一条直线，称作回归线。其中，𝜃1为回归线的斜率， 𝜃0为回归线的截距。

线性回归的三种关系:
1. 正相关
2. 负相关
3. 不相关

求解方程系数

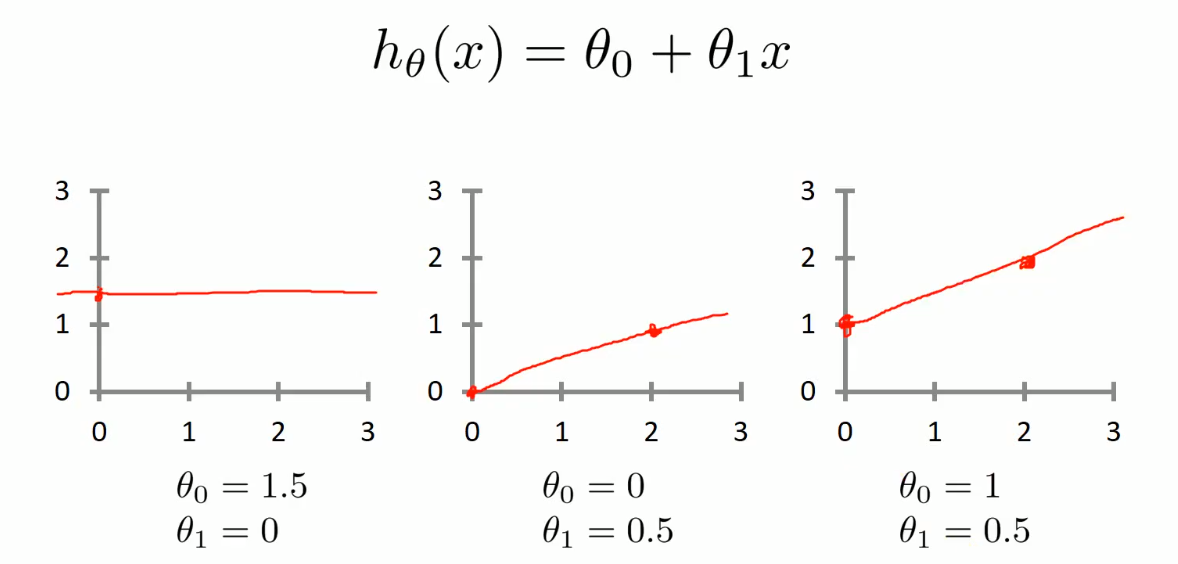
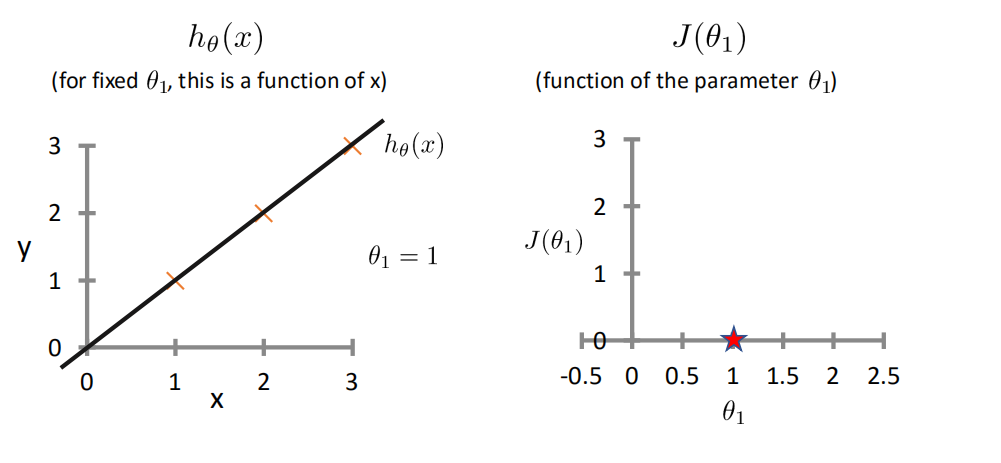
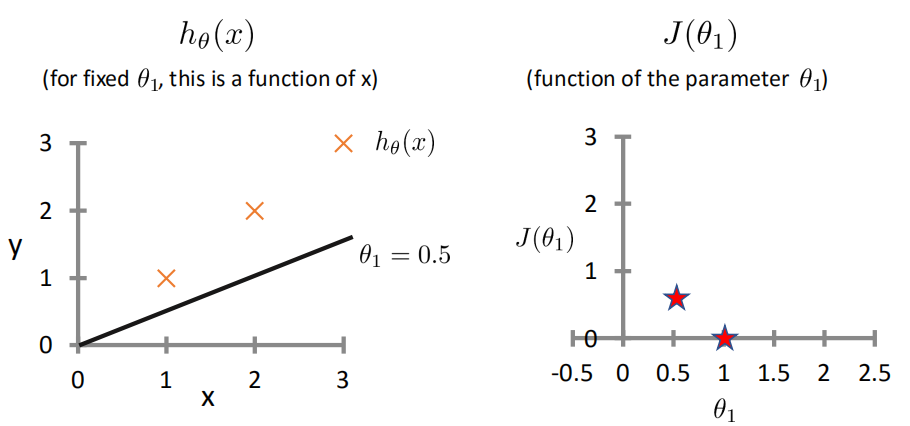
代价函数Cost Function

最小二乘法
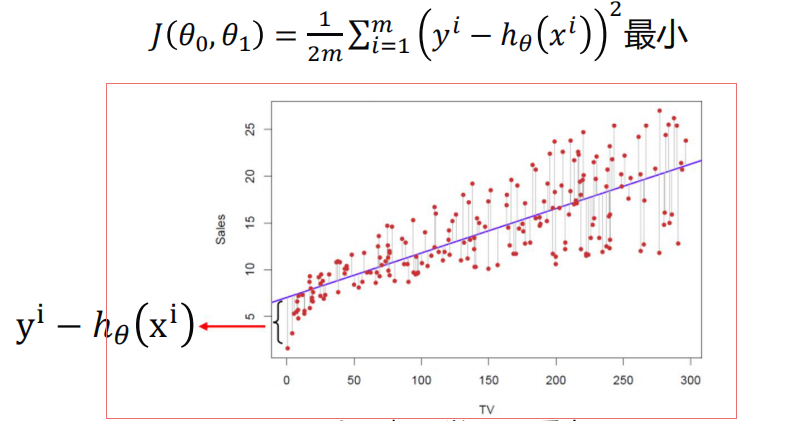
真实值y，预测值ℎ𝜃 𝑥 ，则误差平方为(y − ℎ_𝜃(x))^2
找到合适的参数，使得误差平方和：

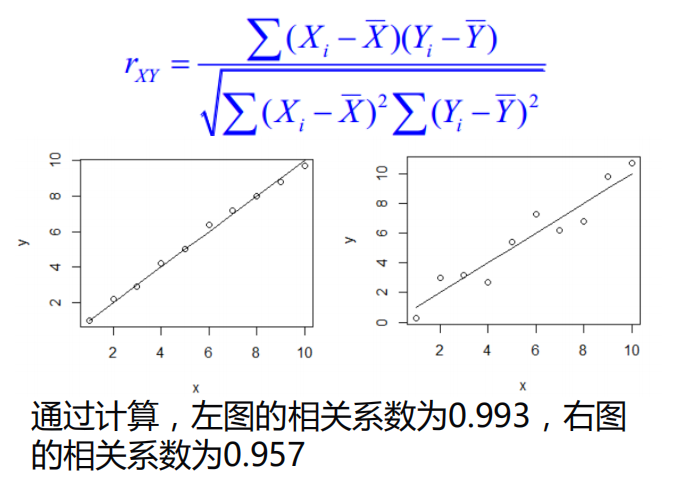
决定系数

相关系数𝑅2(coefficient of determination)是用来描述两个变量之间的线性关系的，但决定系数的适用范围更广，可以用于描述非线性或者有两个及两个以上自变量的相关关系。它可以用来评价模型的效果

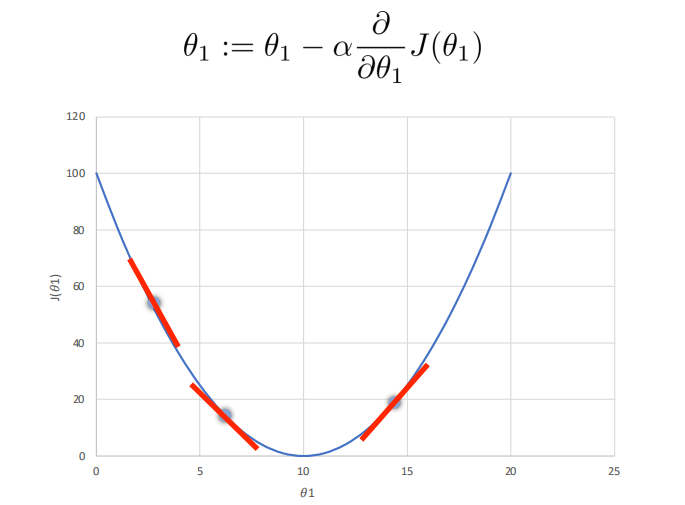
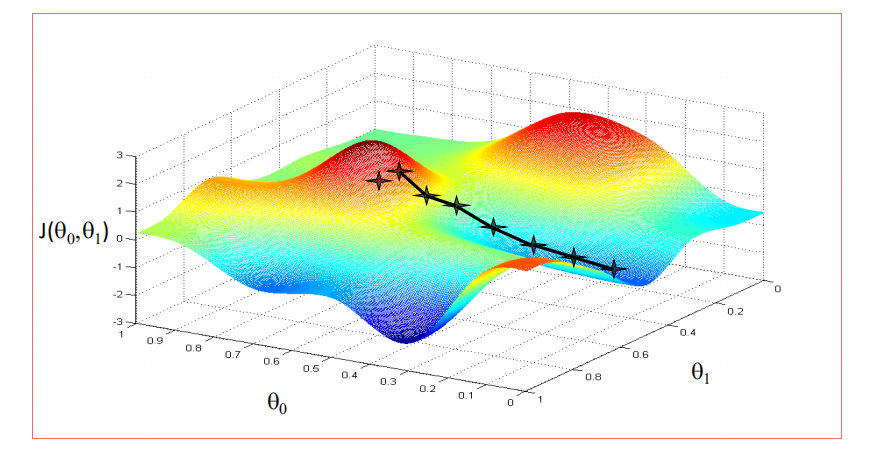
梯度下降法Gradient Descent

学习率不能太小，也不能太大，可以多尝试一些值0.1,0.03,0.01,0.003,0.001,0.0003,0.0001…,否则有可能会陷入局部极小值

用梯度下降法来求解线性回归

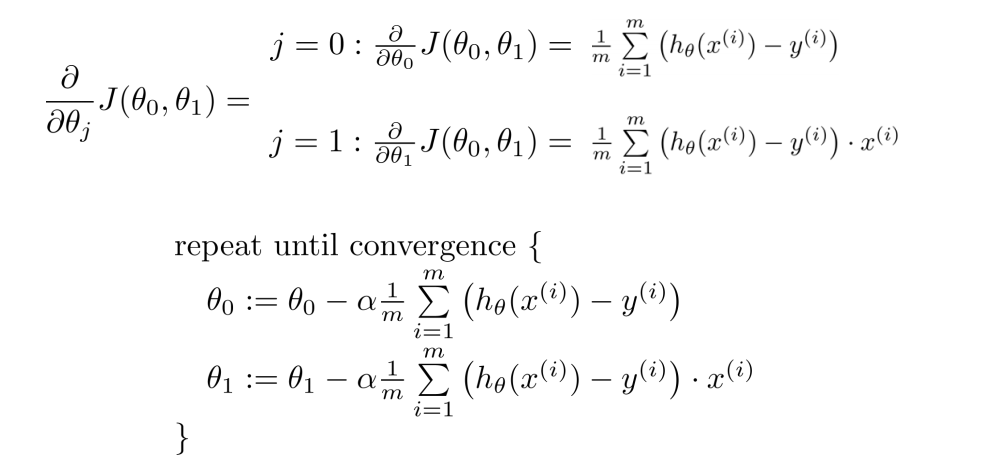
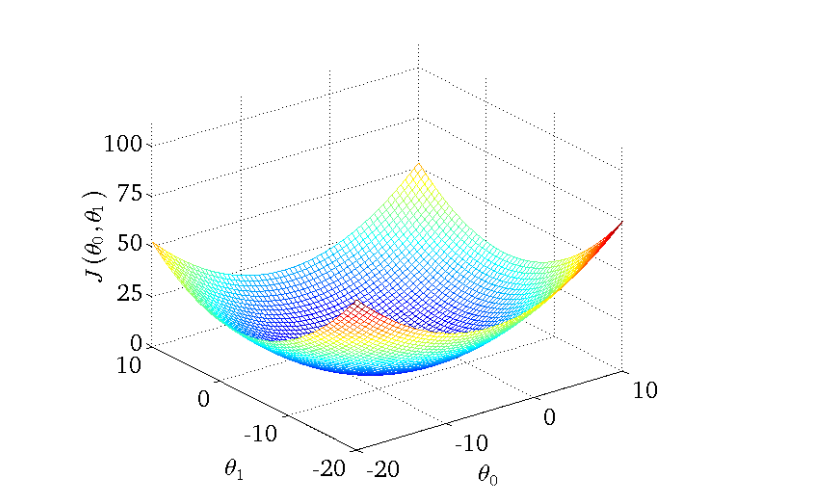
非凸函数和凸函数

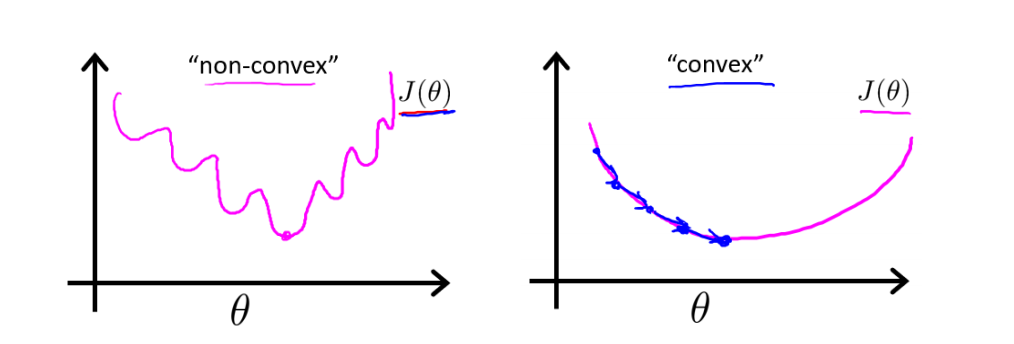
线性回归的代价函数是凸函数

优化过程

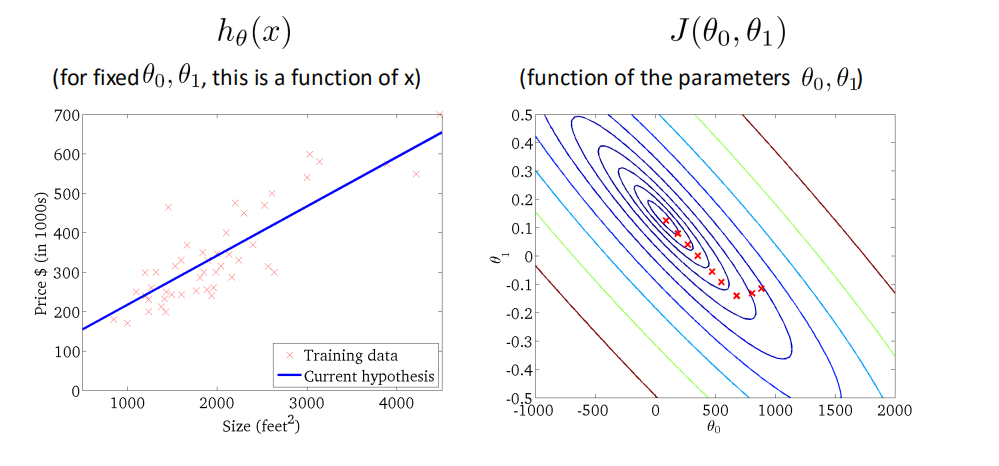
代码实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55


import numpy as np
import matplotlib.pyplot as plt
#载入数据
data = np.genfromtxt("data.csv",delimiter=",")
x_data = data[:,0]
y_data = data[:,1]
plt.scatter(x_data,y_data)
plt.show()
#learning rate
lr = 0.0001
#截距
b = 0
#斜率
k = 0
#最大迭代次数
epochs = 50

#最小二乘法
def compute_error(b, k, x_data, y_data):
    totalError = 0
    for i in range(0,len(x_data)):
        #(真实值-预测值)^2
        totalError += (y_data[i]-(k * x_data[i] + b)) ** 2
    return totalError / float(len(x_data)) / 2

def gradient_descent_runner(x_data, y_data, b, k, lr, epochs):
    #计算总数据量
    m = float(len(x_data))
    for i in range (epochs):
        b_grad = 0
        k_grad = 0
        for j in range (0, len(x_data)):
            b_grad += - (1/m) * (y_data[j] - ((k * x_data[j]) + b))
            k_grad += - (1/m) * x_data[j] * (y_data[j] - ((k * x_data[j]) + b))
        b = b - (lr * b_grad)
        k = k - (lr * k_grad)
        #每迭代五次,输出图像
        if i % 5 == 0:
            print("epochs :",i)
            plt.plot(x_data, y_data, 'b.')
            plt.plot(x_data, k*x_data + b, 'r')
            plt.show()
        
    return b, k


print("Starting b = {0}, k = {1}, error = {2}".format(b, k, compute_error(b, k, x_data, y_data)))
print("Running ...")
b, k = gradient_descent_runner(x_data, y_data, b, k, lr, epochs)
print("After {0} iterations b = {1}, k = {2}, error = {3}".format(epochs, b, k, compute_error(b, k, x_data, y_data)))

# 画图
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, k*x_data + b, 'r')
plt.show()

运行结果

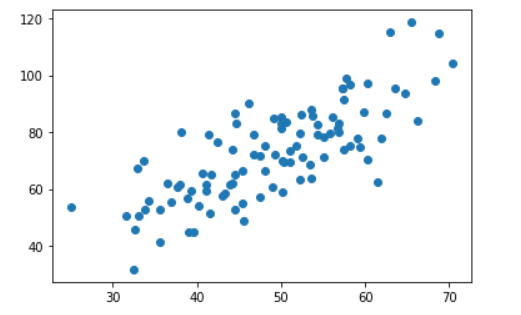
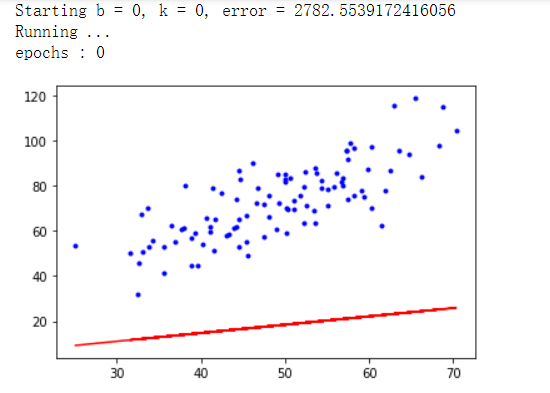
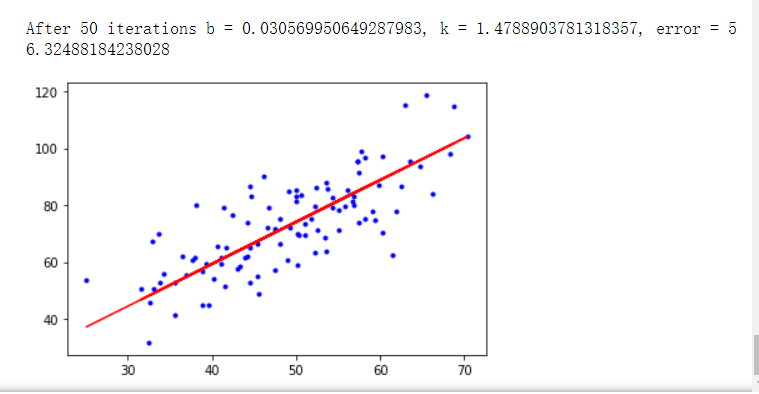
使用sklearn实现-一元线性回归

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


from sklearn. linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
#载入数据
data = np.genfromtxt("data.csv",delimiter=",")
x_data = data[:,0]
y_data = data[:,1]
plt.scatter(x_data,y_data)
plt.show()
print(x_data.shape)
#加上纬度
x_data = data[:,0,np.newaxis]
y_data = data[:,1,np.newaxis]
print(x_data.shape)
print(y_data.shape)
#创建并拟合模型
model = LinearRegression()
model.fit(x_data, y_data)
#画图
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, model.predict(x_data), 'r')
plt.show()

运行结果

基于梯度下降法的多元线性回归应用

多元线性回归

单特征
多特征

多元线性回归模型

当Y值的影响因素不是唯一时，采用多元线性回归

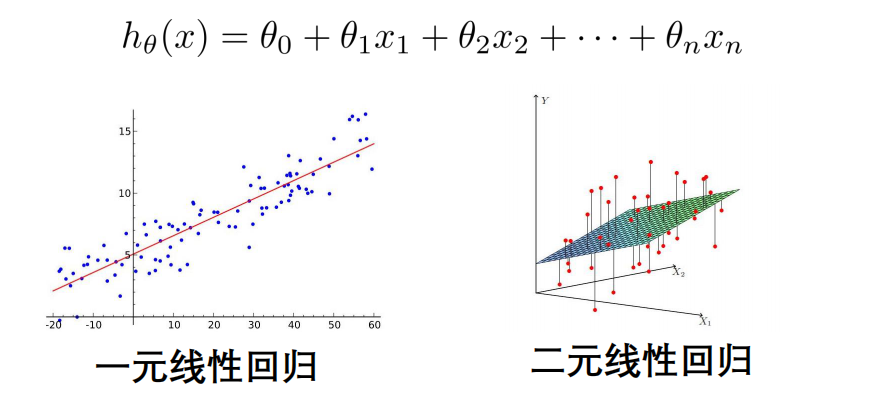
梯度下降法-多元线性回归

代码实现

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103


import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
data = genfromtxt(r"Delivery.csv",delimiter=',')
print(data)
'''
[[100.    4.    9.3]
[ 50.    3.    4.8]
[100.    4.    8.9]
[100.    2.    6.5]
[ 50.    2.    4.2]
[ 80.    2.    6.2]
[ 75.    3.    7.4]
[ 65.    4.    6. ]
[ 90.    3.    7.6]
[ 90.    2.    6.1]]
'''
#切分数据
x_data = data[:,:-1]
y_data = data[:,-1]
print(x_data)
print(y_data)
'''
[[100.   4.]
[ 50.   3.]
[100.   4.]
[100.   2.]
[ 50.   2.]
[ 80.   2.]
[ 75.   3.]
[ 65.   4.]
[ 90.   3.]
[ 90.   2.]]
[9.3 4.8 8.9 6.5 4.2 6.2 7.4 6.  7.6 6.1]
'''
#学习率
lr = 0.0001
#参数
theta0 = 0
theta1 = 0
theta2 = 0
#最大迭代次数
epochs = 1000

#最小二乘法
def compute_error(theta0, theta1, theta2, x_data, y_data):
  totalError = 0
  for i in range(0, len(x_data)):
      totalError += (y_data[i] - (theta1 * x_data[i,0] + theta2 * x_data[i,1] +theta0)) ** 2
  return totalError / float(len(x_data))

def gradient_descent_runner(x_data, y_data, theta0, theta1, theta2, lr, epochs):
  #计算总数据量
  m = float(len(x_data))
  
  for i in range(epochs):
      theta0_grad = 0
      theta1_grad = 0
      theta2_grad = 0
      #计算梯度的总和再求平均
      for j in range(0, len(x_data)):
          theta0_grad += -(1/m) * (y_data[j] - (theta1 * x_data[j,0] + theta2 * x_data[j,1] + theta0))
          theta1_grad += -(1/m) * x_data[j,0] * (y_data[j] - (theta1 * x_data[j,0] + theta2 * x_data[j,1] + theta0))
          theta2_grad += -(1/m) * x_data[j,1] * (y_data[j] - (theta1 * x_data[j,0] + theta2 * x_data[j,1] + theta0)) 
      #更新
      theta0 = theta0 - (lr * theta0_grad)
      theta1 = theta1 - (lr * theta1_grad)
      theta2 = theta2 - (lr * theta2_grad)
  
  return theta0, theta1, theta2

print("Starting theta0 = {0}, theta1 = {1}, theta2 = {2}, error = {3}".
   format(theta0, theta1, theta2, compute_error(theta0, theta1, theta2, x_data, y_data)))
print("Running....")
theta0, theta1, theta2 = gradient_descent_runner(x_data, y_data, theta0, theta1, theta2, lr, epochs)
print("After {0} iterations theta0 = {1}, theta1 = {2}, theta2 = {3}, error = {4}".
   format(epochs, theta0, theta1, theta2, compute_error(theta0, theta1, theta2, x_data, y_data)))

'''
Starting theta0 = 0, theta1 = 0, theta2 = 0, error = 47.279999999999994
Running....
After 1000 iterations theta0 = 0.006971416196678632, theta1 = 0.08021042690771771, theta2 = 0.07611036240566814, error = 0.7731271432218118
'''

ax = plt.figure().add_subplot(111, projection = '3d')
ax.scatter(x_data[:,0], x_data[:,1], y_data, c = 'r', marker = 'o', s = 100)

x0 = x_data[:,0]
x1 = x_data[:,1]

#生成网格矩阵
x0, x1 = np.meshgrid(x0, x1)
z = theta0 + x0 * theta1 + x1 * theta2
#画3D图
ax.plot_surface(x0, x1, z)
#设置坐标轴
ax.set_xlabel("Miles")
ax.set_ylabel('Num of Deleveries')
ax.set_zlabel('Time')

#显示
plt.show()

运行结果

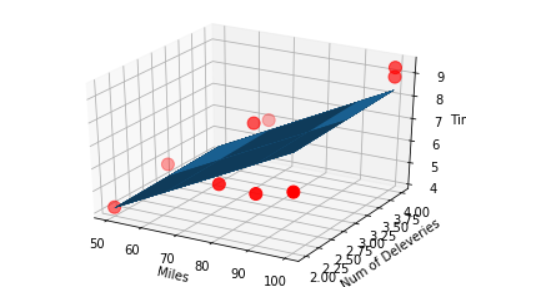
基于sklearn实现多元线性回归

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46


from sklearn import linear_model 
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

data = genfromtxt(r"Delivery.csv",delimiter=',')
print(data)

#切分数据
x_data = data[:,:-1]
y_data = data[:,-1]

#创建模型
model = linear_model.LinearRegression()
model.fit(x_data,y_data)

#系数
print("coefficients:",model.coef_)

#截距
print("intercept:",model.intercept_)

#测试
x_test = [[102,4]]
predict = model.predict(x_test)
print("predict:",predict)

ax = plt.figure().add_subplot(111, projection = '3d')
ax.scatter(x_data[:,0], x_data[:,1], y_data, c = 'r', marker = 'o', s = 100)

x0 = x_data[:,0]
x1 = x_data[:,1]

#生成网格矩阵
x0, x1 = np.meshgrid(x0, x1)
z = model.intercept_ + x0 * model.coef_[0] + x1 * model.coef_[1]
#画3D图
ax.plot_surface(x0, x1, z)
#设置坐标轴
ax.set_xlabel("Miles")
ax.set_ylabel('Num of Deleveries')
ax.set_zlabel('Time')

#显示
plt.show()

运行结果与上面类似,就不展示出来了

多项式回归及应用

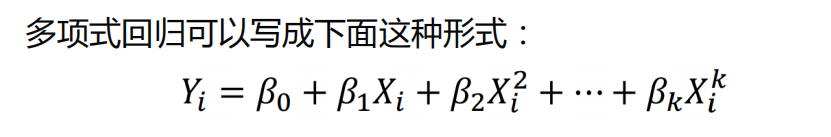
代码实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.lineaBr_model import LinearRegression

#载入数据
data = np.genfromtxt("job.csv",delimiter=",")
x_data = data[1:,1]
y_data = data[1:,2]
plt.scatter(x_data, y_data)
plt.show()

x_data = x_data[:,np.newaxis]
y_data = y_data[:,np.newaxis]
#创建并拟合模型
#这里是多元线性回归
model = LinearRegression()
model.fit(x_data, y_data)
#画图
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, model.predict(x_data), 'r')
plt.show()

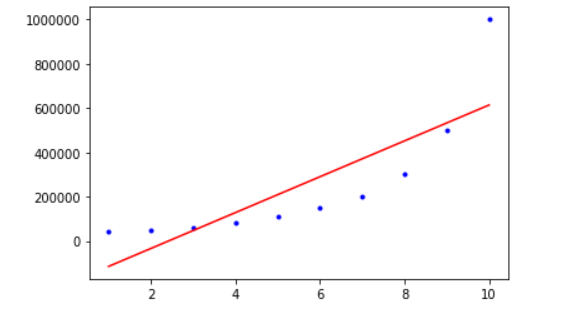
可以看出使用多元线性回归,效果并不是太好,所以我们换成多项式回归来对数据进行特征处理一下

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


#定义多项式回归,degree(偏置值)的值可以调节多项式的特征
poly_reg = PolynomialFeatures(degree = 5)
#特征处理
x_poly = poly_reg.fit_transform(x_data)
print(x_poly)
#定义回归模型
lin_reg = LinearRegression()
#训练模型
lin_reg.fit(x_poly, y_data)

#画图
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, lin_reg.predict(poly_reg.fit_transform(x_data)), c='r')
plt.title("Truth of Bluff (Polynomial Regression)")
plt.xlabel("Position level")
plt.ylabel("Salary")
plt.show()

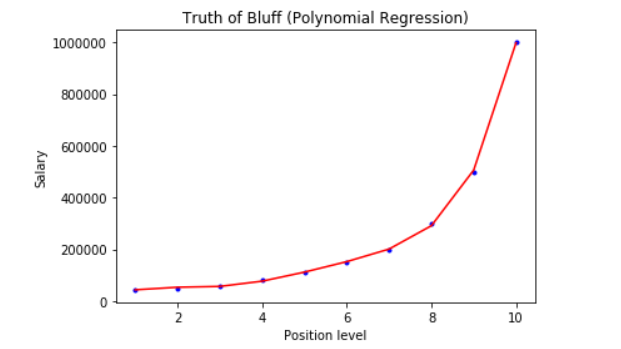
这里看到通过进行多项式特征处理后,拟合结果就比较好

标准方程法(Normal Equation)

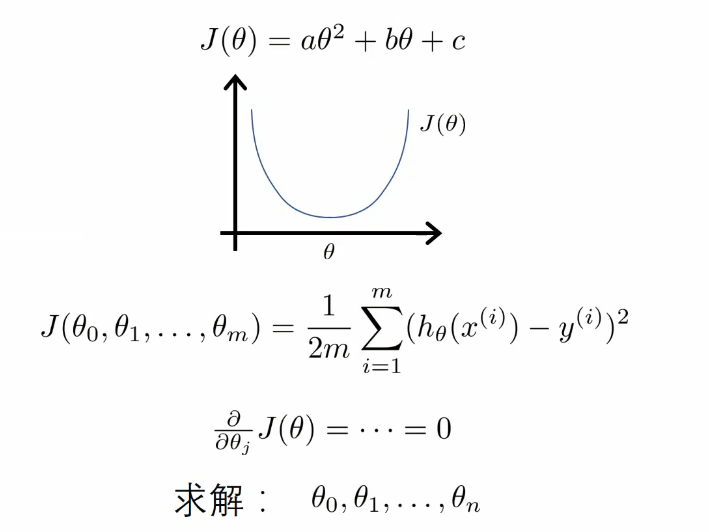
分子布局(Numerator-layout): 分子为列向量或者分母为行向量

分母布局(Denominator-layout):分子为行向量或者分母为列向量

求导公式:https://en.wikipedia.org/wiki/Matrix_calculus#Scalar-by-vector_identiti

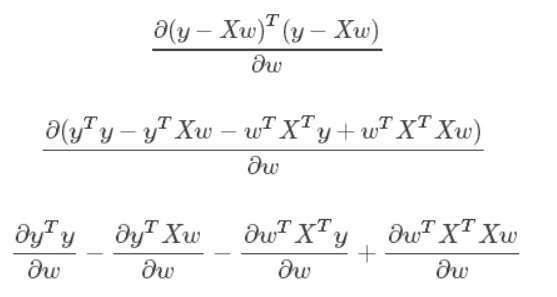
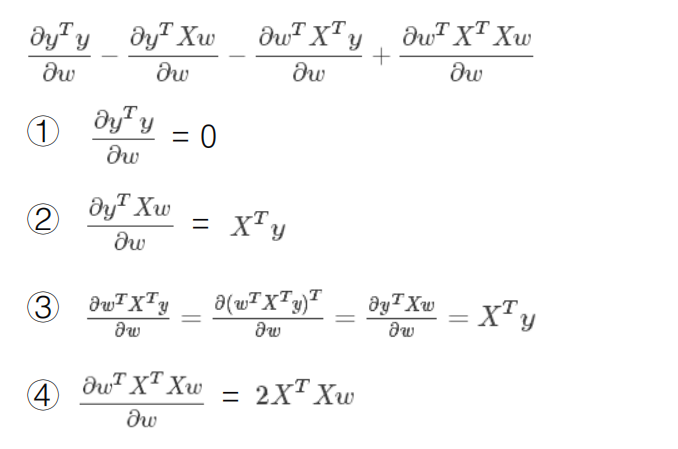
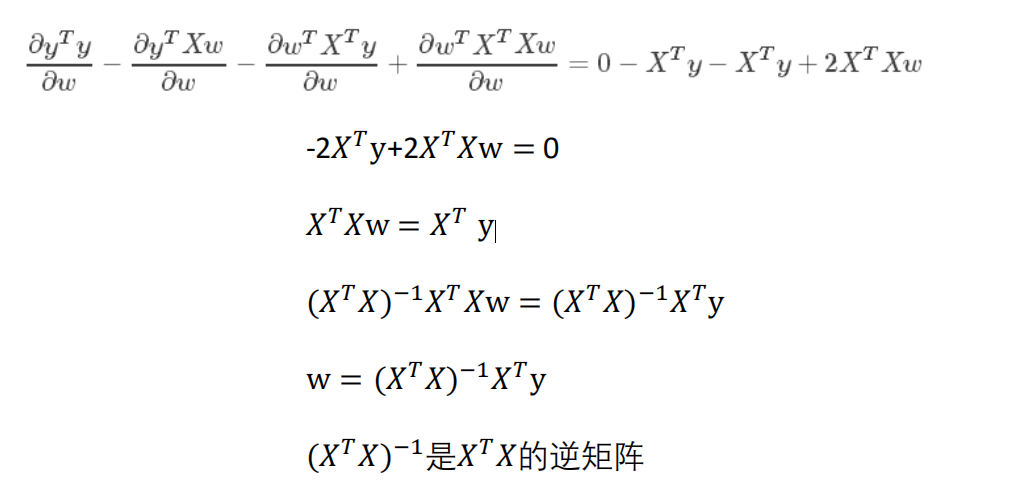
矩阵不可逆的情况

线性相关的特征(多重共线性)
特征数据太多(样本数m<=特征数量n)

梯度下降法vs标准方程法

代码实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48


import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt

#标准方程法求解回归参数
def weights(xArr, yArr):
    xMat = np.mat(xArr)
    yMat = np.mat(yArr)
    xTx = xMat.T * xMat #矩阵乘法
    #计算矩阵的值,如果值为0,说明该矩阵没有逆矩阵
    if np.linalg.det(xTx) == 0.0 :
        print("This matrix cannot do inverse")
        return
    #xTx.T 为 xTx 的逆矩阵
    ws = xTx.I * xMat.T * yMat
    return ws


#载入数据
data = np.genfromtxt("data.csv",delimiter=",")
x_data = data[:,0, np.newaxis]
y_data = data[:,1, np.newaxis]
plt.scatter(x_data, y_data)
plt.show()

#给样本添加偏置项
X_data = np.concatenate((np.ones((100,1)), x_data), axis=1)
print(X_data.shape)

​```
(100, 2)
​```

ws = weights(X_data, y_data)
print(ws)

​```
[[7.99102098]
 [1.32243102]]
​```

#画图
x_test = np.array(([20],[80]))
y_test = ws[0] + x_test*ws[1]
y_data_predict = ws[0] + x_data*ws[1]
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, y_data_predict, 'r')
plt.show()

运行结果

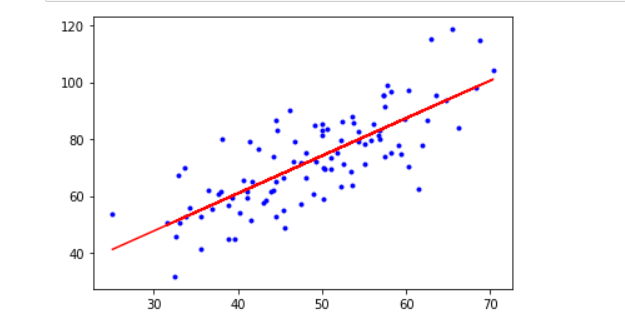
特征缩放交叉验证法

特征缩放

数据归一化:

数据归一化就是把数据的取值范围处理为0-1或者-1-1之间。

任意数据转化为0-1之间：newValue = (oldValue-min)/(max-min)

任意数据转化为-1-1之间：newValue = ((oldValue-min)/(max-min)-0.5)*2

均值标准化:

x为特征数据，u为数据的平均值，s为数据的方差

newValue = (oldValue-u)/s

交叉验证法

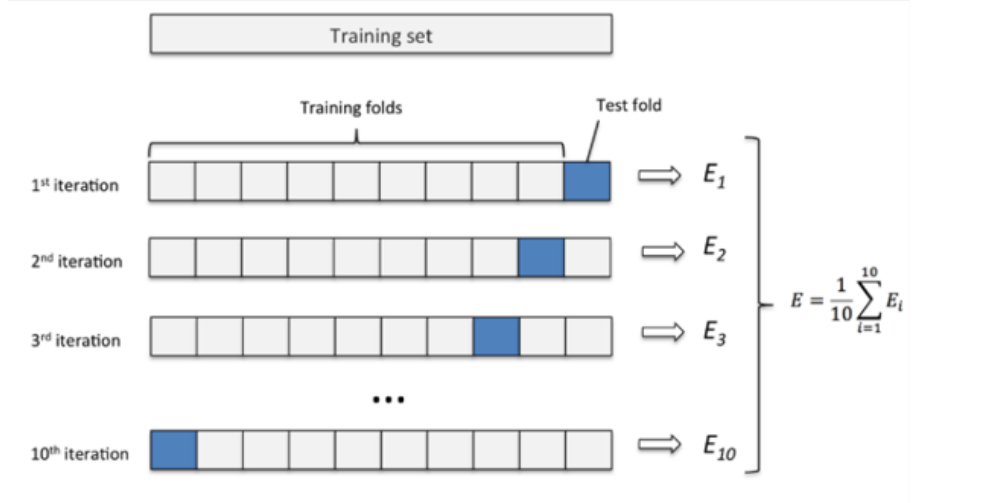
通过切分数据,每个部分分成训练集和测试集,且将每个部分的误差加起来计算平均值即为最终误差

过拟合(Overfitting)&正则化(Regularized)

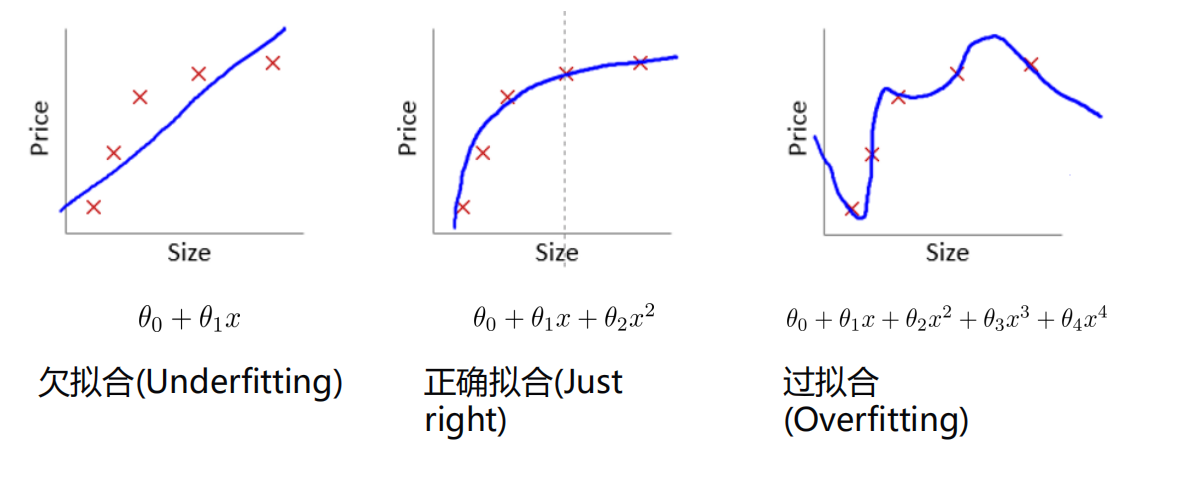
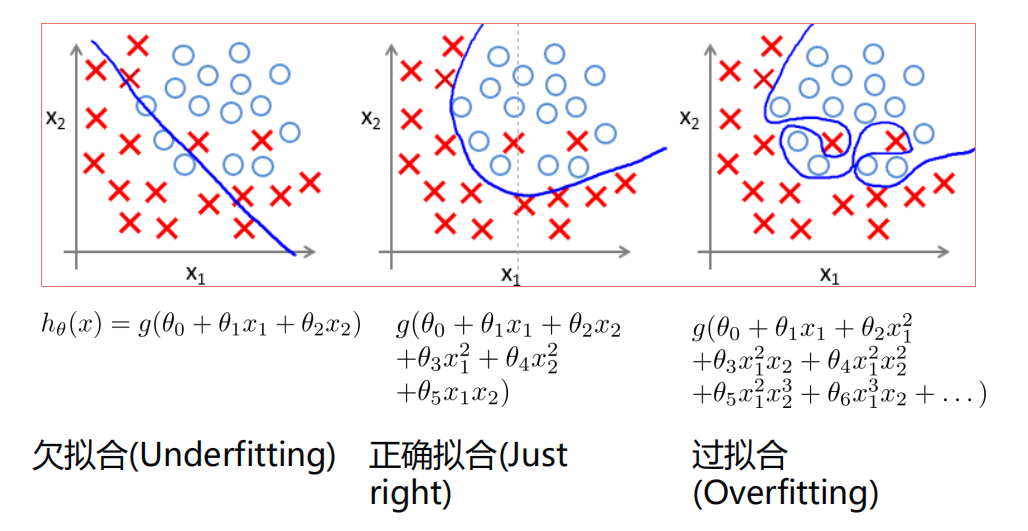
过拟合

拟合情况:

防止过拟合:

减少特征
增加数据量
正则化

正则化

岭回归/LASSO回归/弹性网的应用

岭回归(Ridge Regression)

w = (𝑋^𝑇𝑋)^(−1)𝑋^𝑇y

如果数据的特征比样本点还多，数据特征n，样本个数m，如果n>m，则计算时会出错。因为(𝑋^𝑇𝑋)不是满秩矩阵，所以不可逆。

为了解决这个问题，统计学家引入了岭回归的概念。

岭回归最早是用来处理特征数多于样本的情况，现在也用于在估计中加入偏差，从而得到更好的估计。同时也可以解决多重共线性的问题。岭回归是一种有偏估计。

选择𝜆值，使到：

各回归系数的岭估计基本稳定。
残差平方和增大不太多

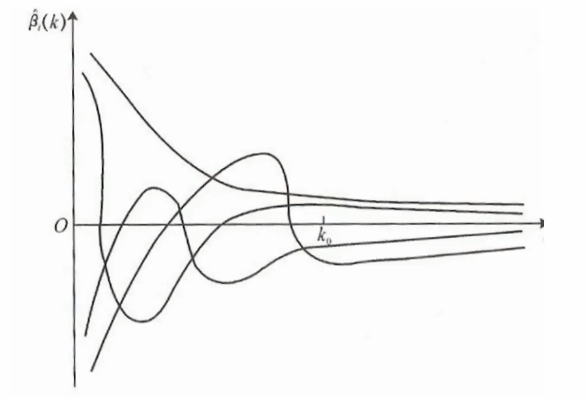
𝜆值为横坐标,所求参数为纵坐标

sklearn-代码实现

Longley数据集

Longley数据集来自J．W．Longley（1967）发表在JASA上的一篇论文，是强共线性的宏观经济数据,包含GNP deflator(GNP平减指数)、GNP(国民生产总值)、Unemployed(失业率)、ArmedForces(武装力量)、Population(人口)、year(年份)，Emlpoyed(就业率)。

LongLey数据集因存在严重的多重共线性问题，在早期经常用来检验各种算法或计算机的计算精度

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64


import numpy as np
from numpy import genfromtxt
from sklearn import linear_model
import matplotlib.pyplot as plt

#载入数据
data = genfromtxt(r"longley.csv", delimiter=',')
print(data)

​```
[[     nan      nan      nan      nan      nan      nan      nan      nan]
 [     nan   83.     234.289  235.6    159.     107.608 1947.      60.323]
 [     nan   88.5    259.426  232.5    145.6    108.632 1948.      61.122]
 [     nan   88.2    258.054  368.2    161.6    109.773 1949.      60.171]
 [     nan   89.5    284.599  335.1    165.     110.929 1950.      61.187]
 [     nan   96.2    328.975  209.9    309.9    112.075 1951.      63.221]
 [     nan   98.1    346.999  193.2    359.4    113.27  1952.      63.639]
 [     nan   99.     365.385  187.     354.7    115.094 1953.      64.989]
 [     nan  100.     363.112  357.8    335.     116.219 1954.      63.761]
 [     nan  101.2    397.469  290.4    304.8    117.388 1955.      66.019]
 [     nan  104.6    419.18   282.2    285.7    118.734 1956.      67.857]
 [     nan  108.4    442.769  293.6    279.8    120.445 1957.      68.169]
 [     nan  110.8    444.546  468.1    263.7    121.95  1958.      66.513]
 [     nan  112.6    482.704  381.3    255.2    123.366 1959.      68.655]
 [     nan  114.2    502.601  393.1    251.4    125.368 1960.      69.564]
 [     nan  115.7    518.173  480.6    257.2    127.852 1961.      69.331]
 [     nan  116.9    554.894  400.7    282.7    130.081 1962.      70.551]]
​```

#切分数据
x_data = data[1:,2:]
y_data = data[1:,1]

#创建模型
#生成50个值
alphas_to_test = np.linspace(0.001, 1)
#创建模型,保存误差值,CV:交叉验证
model = linear_model.RidgeCV(alphas = alphas_to_test, store_cv_values= True)
model.fit(x_data, y_data)

#岭系数
print(model.alpha_)
#loss值
print(model.cv_values_.shape)

​```
0.40875510204081633
(16, 50)
​```

#画图
#岭系数跟Loss值的关系
plt.plot(alphas_to_test, model.cv_values_.mean(axis=0))
#选取的岭系数的位置
plt.plot(model.alpha_, min(model.cv_values_.mean(axis=0)), 'ro')
plt.show()

#简单测试
model.predict(x_data[2,np.newaxis])
y_data[2]
​```
out:array([88.11216213])
out:88.2
​```

运行结果

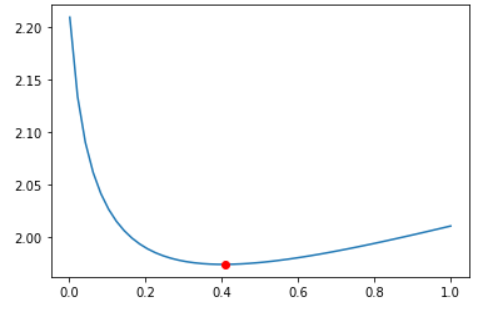
标准方程法-代码实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94


import numpy as np
from numpy import genfromtxt
from sklearn import linear_model
import matplotlib.pyplot as plt

#载入数据
data = genfromtxt(r"longley.csv", delimiter=',')
print(data)
#切分数据
x_data = data[1:,2:]
y_data = data[1:,1,np.newaxis]
print(x_data.shape)
print(y_data.shape)

​```
[[     nan      nan      nan      nan      nan      nan      nan      nan]
 [     nan   83.     234.289  235.6    159.     107.608 1947.      60.323]
 [     nan   88.5    259.426  232.5    145.6    108.632 1948.      61.122]
 [     nan   88.2    258.054  368.2    161.6    109.773 1949.      60.171]
 [     nan   89.5    284.599  335.1    165.     110.929 1950.      61.187]
 [     nan   96.2    328.975  209.9    309.9    112.075 1951.      63.221]
 [     nan   98.1    346.999  193.2    359.4    113.27  1952.      63.639]
 [     nan   99.     365.385  187.     354.7    115.094 1953.      64.989]
 [     nan  100.     363.112  357.8    335.     116.219 1954.      63.761]
 [     nan  101.2    397.469  290.4    304.8    117.388 1955.      66.019]
 [     nan  104.6    419.18   282.2    285.7    118.734 1956.      67.857]
 [     nan  108.4    442.769  293.6    279.8    120.445 1957.      68.169]
 [     nan  110.8    444.546  468.1    263.7    121.95  1958.      66.513]
 [     nan  112.6    482.704  381.3    255.2    123.366 1959.      68.655]
 [     nan  114.2    502.601  393.1    251.4    125.368 1960.      69.564]
 [     nan  115.7    518.173  480.6    257.2    127.852 1961.      69.331]
 [     nan  116.9    554.894  400.7    282.7    130.081 1962.      70.551]]
(16, 6)
(16, 1)
​```

print(np.mat(x_data).shape)
print(np.mat(y_data).shape)
#给样本项加偏置值
X_data = np.concatenate((np.ones((16,1)), x_data),axis=1)
print(X_data.shape)

​```
(16, 6)
(16, 1)
(16, 7)
​```

#岭回归标准方程法求解回归参数
def weights(xArr, yArr, lam=0.2):
    xMat = np.mat(xArr)
    yMat = np.mat(yArr)
    xTx = xMat.T * xMat #矩阵乘法
    rxTx = xTx + np.eye(xMat.shape[1]) * lam
    if np.linalg.det(rxTx) == 0.0:
        print("This mattrix cannot do inverse")
        return
    ws = rxTx.I * xMat.T * yMat
    return ws

ws = weights(X_data, y_data)
print(ws)

​```
[[ 7.38107882e-04]
 [ 2.07703836e-01]
 [ 2.10076376e-02]
 [ 5.05385441e-03]
 [-1.59173066e+00]
 [ 1.10442920e-01]
 [-2.42280461e-01]]
​```

#计算预测值
print(np.mat(X_data) * np.mat(ws))

​```
[[ 83.55075226]
 [ 86.92588689]
 [ 88.09720228]
 [ 90.95677622]
 [ 96.06951002]
 [ 97.81955375]
 [ 98.36444357]
 [ 99.99814266]
 [103.26832266]
 [105.03165135]
 [107.45224671]
 [109.52190685]
 [112.91863666]
 [113.98357055]
 [115.29845063]
 [117.64279933]]
​```

LASSO

Tibshirani(1996)提出了Lasso(The Least Absolute Shrinkage and Selectionator operator)算法

通过构造一个一阶惩罚函数获得一个精炼的模型；通过最终确定一些指标（变量）的系数为零（岭回归估计系数等于0的机会微乎其微，造成筛选变量困难），解释力很强。

擅长处理具有多重共线性的数据，与岭回归一样是有偏估计 。

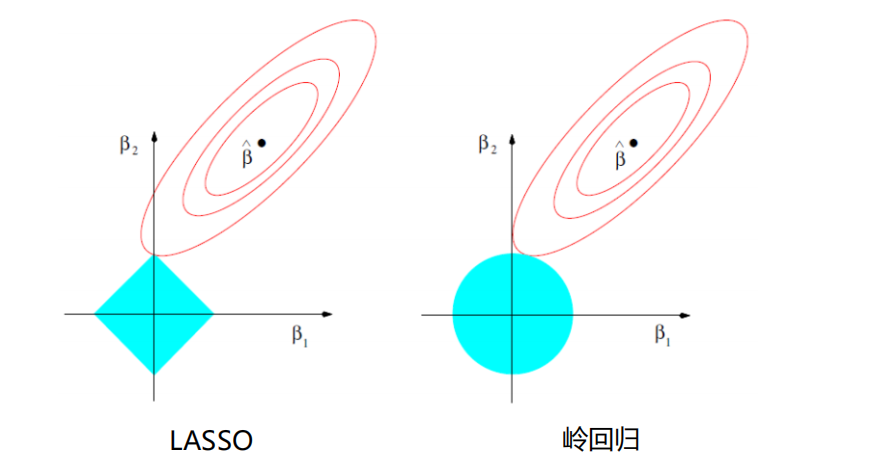
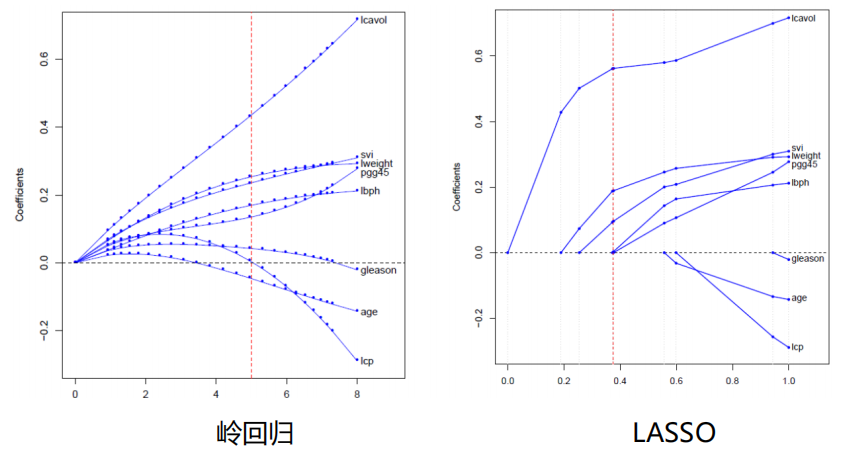
LASSO与岭回归

图像比较

sklearn-代码实现Lasso

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41


import numpy as np
from numpy import genfromtxt
from sklearn import linear_model

#载入数据
data = genfromtxt(r"longley.csv",delimiter = ',')
print(data.shape)
#切分数据
x_data = data[1:,2:]
y_data = data[1:,1]
print(x_data.shape)
print(y_data.shape)
​```
(17, 8)
(16, 6)
(16,)
​```

#创建模型,得到一个合适的误差值,由于交叉验证其函数内部自动生成随机数进行测试
model = linear_model.LassoCV()
model.fit(x_data, y_data)
#lasso系数
print(model.alpha_)
#相关系数
print(model.coef_)
#其中三个特征有共线性即为0

​```
20.03464209711722
[0.10206856 0.00409161 0.00354815 0.         0.         0.        ]
​```

#预测值
print(model.predict(x_data[-2,np.newaxis]))
#真实值
print(y_data[-2])

​```
[115.6461414]
115.7
​```

弹性网(Elastic Net)

很容易看出,q=2时就是为岭回归,q=1为Lasso回归

sklearn-代码实现ElasticNet

由于部分结果与上面类似,这里就不贴出来了

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36


import numpy as np
from numpy import genfromtxt
from sklearn import linear_model

#载入数据
data = genfromtxt(r"longley.csv", delimiter=',')
print(data)
print(data.shape)

#切分数据
x_data = data[1:,2:]
y_data = data[1:,1]

#创建模型
model = linear_model.ElasticNetCV()
model.fit(x_data, y_data)

#l弹性网系数
print(model.alpha_)
#相关系数
print(model.coef_)

​```
42.96498005089394
[0.1016487  0.00416716 0.00349843 0.         0.         0.        ]
​```

#预测值
print(model.predict(x_data[-2,np.newaxis]))
#真实值
print(y_data[-2])

​```
[115.6037171]
115.7
​```

目录

线性回归与非线性回归

基于梯度下降法的一元线性回归应用

回归Regression

一元线性回归

求解方程系数

代价函数Cost Function

相关系数

决定系数

梯度下降法Gradient Descent

用梯度下降法来求解线性回归

非凸函数和凸函数

优化过程

代码实现

运行结果

使用sklearn实现-一元线性回归

运行结果

基于梯度下降法的多元线性回归应用

多元线性回归

多元线性回归模型

梯度下降法-多元线性回归

代码实现

运行结果

基于sklearn实现多元线性回归

多项式回归及应用

代码实现

标准方程法(Normal Equation)

矩阵不可逆的情况

梯度下降法vs标准方程法

代码实现

运行结果

特征缩放交叉验证法

特征缩放

交叉验证法

过拟合(Overfitting)&正则化(Regularized)

过拟合

正则化

岭回归/LASSO回归/弹性网的应用

岭回归(Ridge Regression)

sklearn-代码实现

运行结果

标准方程法-代码实现

LASSO

LASSO与岭回归

sklearn-代码实现Lasso

弹性网(Elastic Net)

sklearn-代码实现ElasticNet