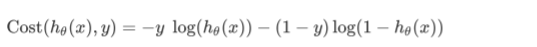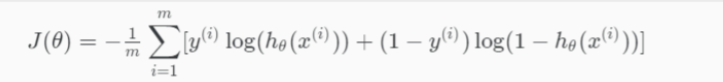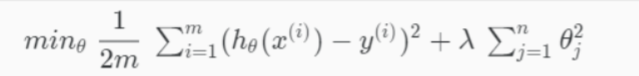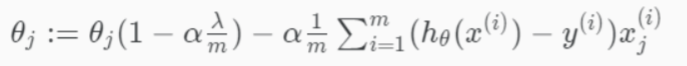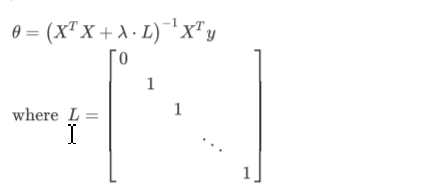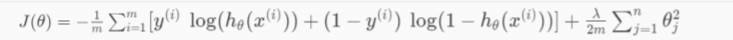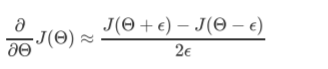MachineLearning(AndrewNg)Notes-Week1-Week5总结

Liner Regression

• Cost Function

  $h(x)=\theta_0+\theta_1x+….$

  $h(x)=\theta^Tx$

• Linear Regression

  $J(\theta) = \frac{1}{2m}\sum_{1}^{m}(h_\theta(x^i)-y^i)$

  $\frac{\partial{J(\theta)}}{\partial{\theta_j}}=\frac{1}{m}\sum_{1}^{m}(h_\theta(x^i)-y^i)$

• Gradient descent algorithm

  repeat until convergence{

  $\theta_j := \theta_j - \frac{ \alpha}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)}) x^{(i)}$

  }

  • Feature scaling and mean normalization

    $x_i=\frac{x_i-\mu_i}{s_i}$

    $\mu_i$: the average of all the values for feature (i)

    $s_i$ : standard deviation

  • learning rate

    If α is too small: slow convergence. If α is too large: may not decrease on every iteration and thus may not converge.

  • Polynomial Regression

    change the behavior or curve of our hypothesis function by making it a quadratic, cubic or square root function (or any other form).

  • Normal Equation

    $\theta = (X^TX)^{-1}X^Ty$

Logistic Regression

• Logistic Function or Sigmoid Function

  

• Decision Boundary

  $\theta^Tx \ge 0 \Rightarrow y=1$

  $\theta^Tx \le 0 \Rightarrow y=0$

• Cost Function

  

• Gradient Descent

  

  • $h=g(X\theta)$

    $J(\theta)=\frac{1}{m}(-y’log(h)-(1-y)’log(1-h))$

  • $\theta:=\theta-\frac{\alpha}{m}X^T(g(\theta X) -y)$

• Advanced Optimization

  1 2 3 4 5 6 7 8

  function [jVal, gradient] = costFunction(theta) jVal = [...code to compute J(theta)...]; gradient = [...code to compute derivative of J(theta)...]; end options = optimset('GradObj', 'on', 'MaxIter', 100); initialTheta = zeros(2,1); [optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);

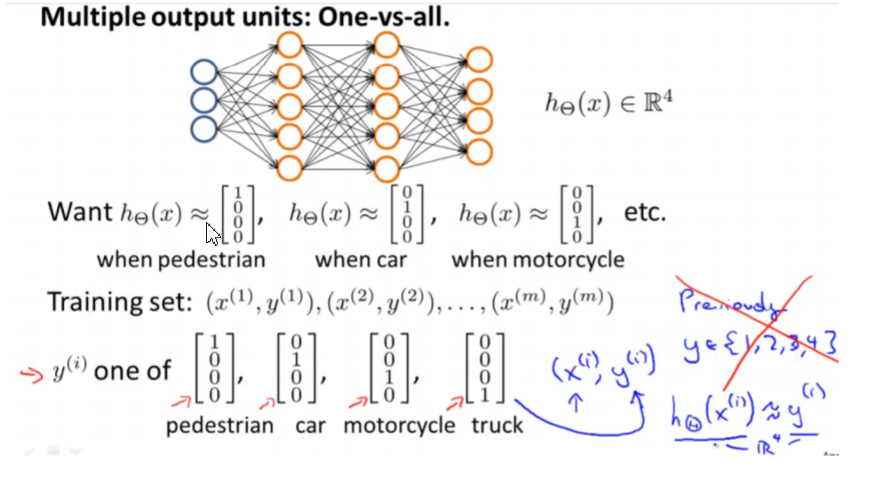
• Multiclass Classification: One-vs-all

  Train a logistic regression classifier $h_\theta(X)$ for each class to predict the probability that y = i . To make a prediction on a new x, pick the class that maximizes $h_\theta(X)$

• Overfitting

  1. Reduce the number of features

  2. Regularization

  

  

  

• Regularized Logistic Regression

  

Neural Networks

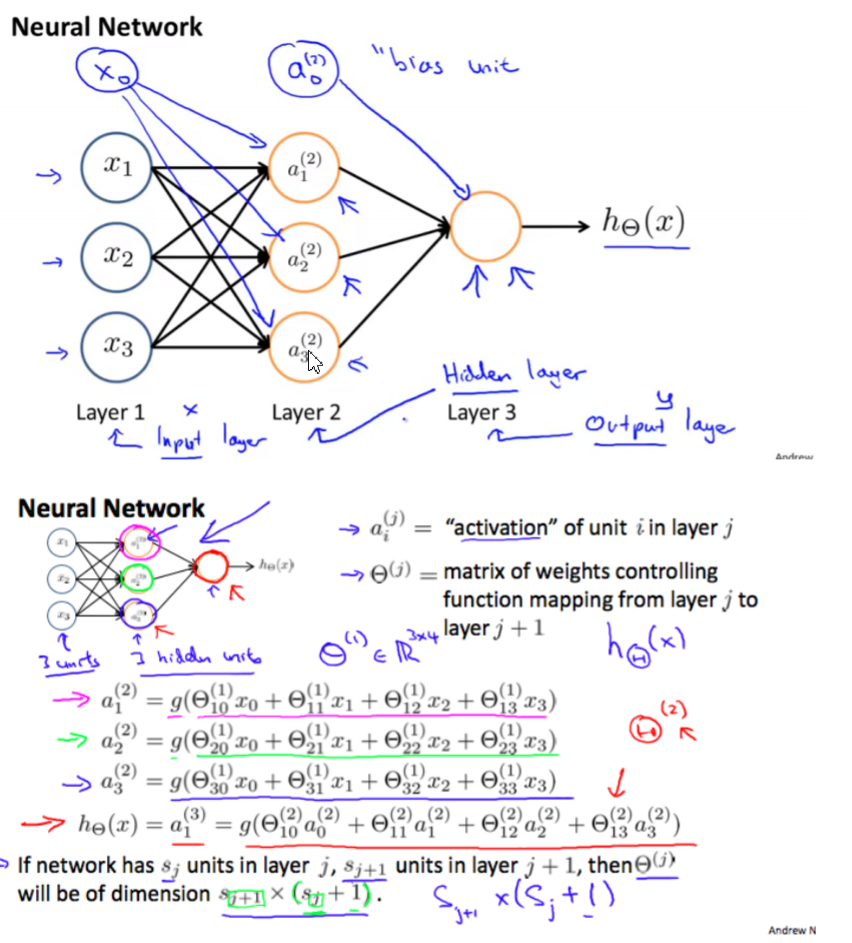
• Model Representation

  • Forward propagation:Vectorized implementation

  

• Multiclass Classification

  one-vs-all

  

• Neural Network(Classification)

  L = total number of layers in the network $s_l$= number of units (not counting bias unit) in layer l K = number of output units/classes

  • Cost Function

    

  • Backpropagation Algorithm

    

  • Gradient Checking

    

  • Random Initialization