《白话机器学习的数学》阅读笔记

概述

通过读取大量的数据、学习数据的特征并从中找出数据的模式。 这样的任务也被称为机器学习或者模式识别。

机器学习中比较擅长的任务：

• 回归（regression）：从连续数据中学习趋势，如时间序列数据；
• 分类（classification）：数据携带标签进行分类；
• 聚类（clustering）：数据本身不带标签；

机器学习中监督学习区分：

• 使用有标签的数据进行的学习称为有监督学习（回归和分类）；
• 使用没有标签的数据进行的学习称为无监督学习（聚类）；

回归问题

$y=\theta_0+\theta_1x$

$f_\theta(x)=\theta_0+\theta_1x$

最小二乘法公式

$$ E(\theta)=\frac{1}{2}\sum_{i=1}^{n}(y^i-f_\theta(x^i))^2 $$

使$y$与$f_\theta(x)$误差尽可能减小即最优化问题，使用差值的平方是因为避免差值为负数同时利于微分，至于$\frac{1}{2}$是为了让作为结果的表达式变得简单而随便加的常数（在最优化问题中不影响结果）。

最速下降法（或梯度下降法）

$$ x:=x-\eta\frac{\mathrm{d}}{\mathrm{d}x}g(x) $$

其中$\eta$即为学习率，可以理解$\eta$越大，则下降越快，更新次数越少，甚至可能远离最优值，这就是发散状态，而$\eta$较小时移动量较小，更新次数增多，但是值会往收敛方向移动。

因为$f_\theta(x)$拥有$\theta_0$和$\theta_1$两个参数，即目标函数是双变量函数，所以不能用普通的微分，而要用偏微分。

$$\theta_0=\theta_0-\eta\frac{\partial{E}}{\partial{\theta_0}}$$

$$\theta_1=\theta_1-\eta\frac{\partial{E}}{\partial{\theta_1}}$$

假设$u=E(\theta)$，$v=f_\theta(x)$，利用阶梯性地进行微分： $$\frac{\partial{u}}{\partial{\theta_0}}=\frac{\partial{u}}{\partial{v}}\cdot\frac{\partial{v}}{\partial{\theta_0}}$$

最后得到：

$$\theta_0=\theta_0-\eta\sum_{i=1}^{n}(f_\theta(x^i)-y^i)$$

$$\theta_1=\theta_1-\eta\sum_{i=1}^{n}(f_\theta(x^i)-y^i)x^i$$

前面我们假设$f_\theta(x)=\theta_0+\theta_1x$，若这里为了更好拟合更新成$f_\theta(x)=\theta_0+\theta_1x+\theta_2x^2$，进行上面类似的梯度计算也可以得到：

$$\theta_0=\theta_0-\eta\sum_{i=1}^{n}(f_\theta(x^i)-y^i)$$

$$\theta_1=\theta_1-\eta\sum_{i=1}^{n}(f_\theta(x^i)-y^i)x^i$$

$$\theta_2=\theta_2-\eta\sum_{i=1}^{n}(f_\theta(x^i)-y^i)x^{i^2}$$

像这样增加函数中多项式的次数，然后再使用函数的分析方法被称为多项式回归。

多重回归

$$f_\theta(x_1,…,x_n)=\theta_0+\theta_1x_1+…+\theta_nx_n$$

将$\theta$和$x$转换为列向量简化表达式：

$$ \mathbf{\theta}=\left[\begin{matrix}\theta_0\\\theta_1\\\vdots\\\theta_n\end{matrix} \right] $$

$$ \mathbf{x}=\left[\begin{matrix}x_0\\x_2\\\vdots\\x_n\end{matrix}\right] $$

得到：$\mathbf{\theta^T}\mathbf{x}=\theta_0x_0+\theta_1x_1+…+\theta_nx_n$ 即 $f_\mathbf{\theta}(\mathbf{x})=\mathbf{\theta^T}\mathbf{x}$

然后我们代入梯度下降算法计算$\theta$的公式：

$$ \theta_j=\theta_j-\eta\sum_{i=1}^{n}(f_\mathbf{\theta}\mathbf{x}^{(i)}-y^{(i)})x{_j}{^{(i)}} $$

随机梯度下降法

前面的最速下降法容易陷入局部最优解的情况：

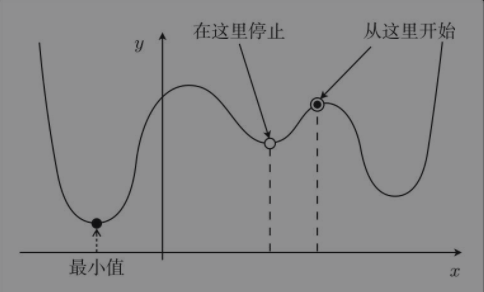
而随机梯度下降法就是训练时随机选择训练数据，设随机选择$m$个训练数据额索引的集合为$K$，那么更新参数的公式为：

$$ \theta_j=\theta_j-\eta\sum_{k\in{K}}(f_\mathbf{\theta}\mathbf{x}^{(k)}-y^{(k)})x{_j}{^{(k)}} $$

分类问题

使权重向量成为法线向量的直线，设权重向量为$\mathbf{w}$，直线的表达式为（向量内积）： $$ \mathbf{w}\cdot\mathbf{x} = 0 $$

或者另外一个内积表达式：$\mathbf{w}\cdot\mathbf{x} = |\mathbf{w}|\cdot|\mathbf{x}|\cdot\cos{\theta}$

通过训练找到权重向量，然后才能得到与这个向量垂直的直线，最后根据这条直线就可以对数据进行分类了。

感知机

接受多个输入后将每个值与各自的权重相乘，最后输出总和的模型。

$$ f_\mathbf{w}(\mathbf{x})=\left\{\begin{array}{ll}1&(\mathbf{w}\cdot\mathbf{x}\geq0)\\-1&(\mathbf{w}\cdot\mathbf{x}<0)\end{array}\right. $$

权重向量的更新表达式：

$$ \mathbf{w}=\left\{\begin{array}{ll}\mathbf{w}+y^{i}\mathbf{x}^{(i)}&&(f_\mathbf{w}(\mathbf{x}^{(i)})\neq y^{(i)})\\\mathbf{w}&&(f_\mathbf{w}(\mathbf{x}^{(i)})= ^{(i)})\end{array}\right. $$

感知机的局限在于只能解决线性可分的问题。

sigmoid函数

$$ f_\theta(\mathbf{x})=\frac{1}{1+e^{-\mathbf{\theta}^{T}\mathbf{x}}} $$

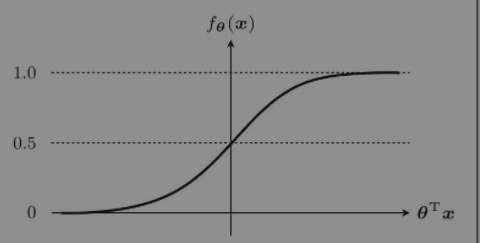
其sigmoid函数取值范围为$0<f_\theta(\mathbf{x})<1$。

其微分结果如下： $\frac{\mathrm{d}\sigma{x}}{\mathrm{d}x}=\sigma{(x)}(1-\sigma{(x)})$

似然函数

目标函数即为通过$P(y=1|\mathbf{x})$和$P(y=0|\mathbf{x})$的联合概率得到：

$$ L(\mathbf{\theta})=\prod_{i=1}^nP(y^{(i)}=1|\mathbf{x}^{(i)})^{y^{(i)}}P(y^{(i)}=0|\mathbf{x}^{(i)})^{1-y^{(i)}} $$

对数似然函数

将似然函数进行对数化便于运算，公式如下：

$$ \log{L(\mathbf{\theta})}=\sum_{i=1}^n(y^{(i)}\log{f_\mathbf{\theta}(\mathbf{x}^{(i)})}+(1-y^{(i)})\log{(1-f_\mathbf{\theta}(\mathbf{x}^{(i)}}))) $$

逻辑回归将这个对数似然函数用作目标函数，然后对目标函数求微分得到：

$$ \frac{\partial{u}}{\partial{\theta_j}}=\frac{\partial{u}}{\partial{v}}\cdot\frac{\partial{v}}{\partial{\theta_j}}=\sum_{i=1}^{n}(y^{(i)}-f_\mathbf{\theta}(\mathbf{x}^{(i)}))x_j^{(i)} $$

最后导出参数更新表达式（梯度下降），这里求的是最大化与之前最小化不同，所以其方向相反：

$$ \theta_j:=\theta_j+\eta\sum_{i=1}^{n}(y^{(i)}-f_\mathbf{\theta}(\mathbf{x}^{(i)}))x_j^{(i)} $$

若与前面回归保持一致即：

$$ \theta_j:=\theta_j-\eta\sum_{i=1}^{n}(f_\mathbf{\theta}(\mathbf{x}^{(i)})-y^{(i)})x_j^{(i)} $$

线性不可分

类似多项回归一样，增加次数得到非线性曲线。

模型评估

交叉验证

将获取的全部训练数据分成两份，一份用于测试，一份用于训练。然后用前者来评估模型。（交叉验证）

回归

对于回归的情况，只要在训练好的模型上计算测试数据的误差的平方，再取其平均值就可以了：

$$ \frac{1}{n}\sum_{i=1}^n(y^{(i)}-f_\mathbf{\theta}(\mathbf{x}^{(i)}))^2 $$

上面得到的值被称为均方误差或者MSE（Mean Square Error）。这个误差越小，精度就越高，模型也就越好。

分类

对于分类的情况，由于回归是连续值，所以可以从误差入手，但是分类中必须考虑分类的类别是否正确。

对于二分类的结果可以用这张图表示：

通过表中的4个记号来表示精度（Accuracy）,表达式如下，即值越高精度越高，也就意味着模型越好：

$$ Accuracy = \frac{TP+TN}{TP+FP+FN+TN} $$

在大多情况下，除了精度还需要引入其他指标进行评估：

• 精确率（$Precision=\frac{TP}{TP+FP}=\frac{TN}{TN+FN}$，值越高分类错误越少)
• 召回率（$Recall=\frac{TP}{TP+FN}=\frac{TN}{TN+FP}$，值越高即被正确分类的数据越多）

当数据不平衡时，使用数量少的那个会更好。

一般来说，精确率和召回率会一个高一个低，需要取舍。基于此就出现了评定综合性能的指标$F1$值，表达式如下：

$F1$值指标在数学上是精确率和召回率的调和平均值。

$$ Fmeasure=\frac{2}{\frac{1}{Precision}+\frac{1}{Recall}} $$

除$F1$值指标外，还有较为通用的带权重的$F$值指标，表达式如下：

$$ WeightedFmeasure = \frac{(1+\beta^2)\cdot Precision\cdot Recall}{\beta^2\cdot Precision+Recall} $$

交叉验证方法

在交叉验证的方法中，较为经典的是K折交叉验证:

• 把全部训练数据分为K份；
• 将K-1份数据用作训练数据，剩下的1份用作测试数据；
• 每次更换训练数据和测试数据，重复进行K次交叉验证；
• 最后计算K个精度的平均值，把它作为最终的精度；

不切实际地增加K值会非常耗费时间，所以必须要确定一个合适的K值。

正则化

过拟合

若模型只能拟合训练数据的状态被称为过拟合（overfitting）。

避免过拟合的方法一般有：

• 增加全部训练数据的数量
• 使用简单的模型
• 正则化

正则化方法

可以在前面回归得到的目标函数（最小二乘法）加上正则化项得到一个新的目标函数，如下：

$$ E(\mathbf{\theta})=\frac{1}{2}\sum_{i=1}^{n}{(y^i-f_\mathbf{\theta}(\mathbf{x}^i))^2}+R(\mathbf{\theta})=\frac{1}{2}\sum_{i=1}^{n}{(y^i-f_\mathbf{\theta}(\mathbf{x}^i))^2}+\frac{\lambda}{2}\sum_{j=1}^{m}\theta_j^2 $$

要对这个新的目标函数进行最小化，这种方法即称为正则化。

其中正则化项中：

• $m$：参数的个数;
• $\theta_0$称为偏置项，一般不对它进行正则化；
• $\lambda$：决定正则化项影响程度的正的常数；

正则化的效果可以防止参数变得过大，有助于参数接近较小的值。参数的值变小，意味着该参数的影响也会相应地变小。

分类的正则化

在前面分类提到的目标函数（对数似然函数）增加正则化项，表达式如下：

$$ \log{L(\mathbf{\theta})}=-\sum_{i=1}^n(y^{(i)}\log{f_\mathbf{\theta}(\mathbf{x}^{(i)})}+(1-y^{(i)})\log{(1-f_\mathbf{\theta}(\mathbf{x}^{(i)}})))+\frac{\lambda}{2}\sum_{j=1}^{m}\theta_j^2 $$

为方便与回归处理相似，将目标函数最大化的目标转化为最小化问题，在原目标函数增加负号，加上正则化项。且这里反转了符号之后，在更新参数时也需要将符号反方向移动。

包含正则化项的表达式的微分

其中回归和分类的目标函数的微分我们在前面已经求过了，这里主要是求正则化项的微分表达式:

$$ \frac{\partial{R(\mathbf{\theta})}}{\partial{\theta_j}}=\lambda\theta_j $$

最后这里代入到回归场景下的参数更新表达式中：

$$ \theta_j:=\theta_j-\eta\big (\sum_{i=1}^{n}(f_\mathbf{\theta}(\mathbf{x}^{(i)})-y^{(i)})x_j^{(i)}+\lambda\theta_j\big ) $$

这里一般不对$\theta_0$应用正则化，所以这里区分两种情况：

• $j=0$

$$ \theta_0:=\theta_0-\eta\big (\sum_{i=1}^{n}(f_\mathbf{\theta}(\mathbf{x}^{(i)})-y^{(i)})x_j^{(i)}\big ) $$

• $j>0$

$$ \theta_j:=\theta_j-\eta\big (\sum_{i=1}^{n}(f_\mathbf{\theta}(\mathbf{x}^{(i)})-y^{(i)})x_j^{(i)}+\lambda\theta_j\big ) $$

至此提到的正则被称为L2正则化，除此之外还有L1正则化，它的正则化项如下：

$$ R(\mathbf{\theta})= \lambda\sum_{i=1}^{m}|\theta_i| $$

L1正则化的特征是被判定为不需要的参数会变为0，从而减少变量个数即直接去除不要的变量。而L2正则化不会把参数变为0，通过会抑制参数，使变量的影响不会过大。

学习曲线

欠拟合

欠拟合（underfitting）与过拟合相反的状态即没有拟合训练数据。在这种情况下模型的性能也会变差。

区分过拟合与欠拟合

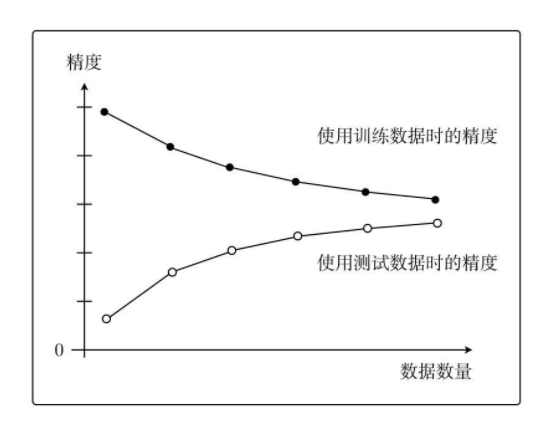
将两份数据的精度用图来展示后，如果是这种形状，就说明出现了欠拟合的状态，也可以称为高偏差。

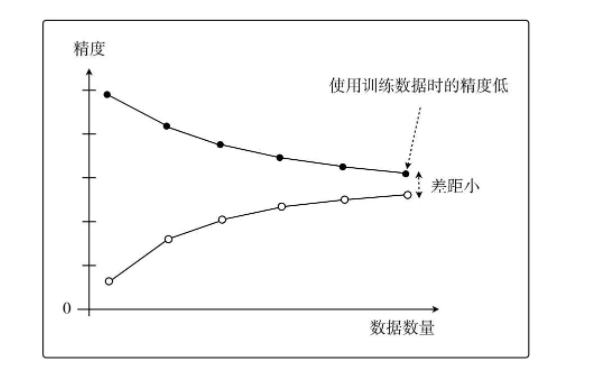
而过拟合或称为高方差，如下图所示：

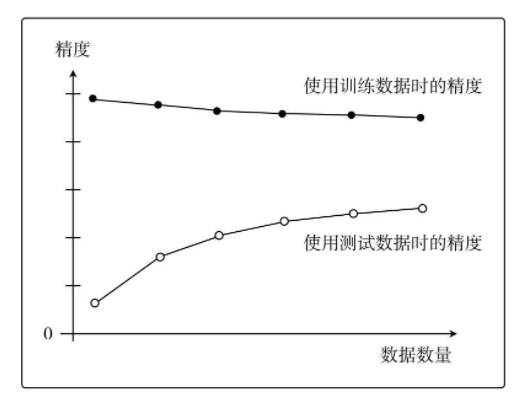
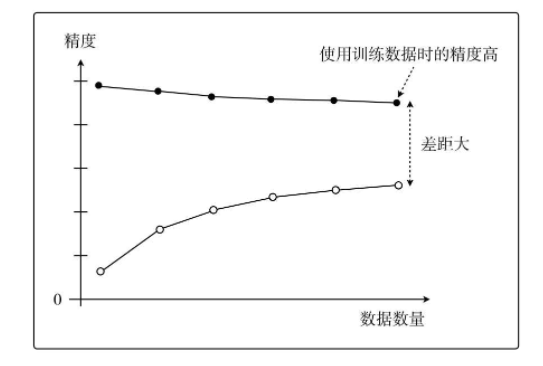
像这样展示了数据数量和精度的图称为学习曲线。