链表算法题目¶

1. 移除链表元素¶

对应 LeetCode 题目：

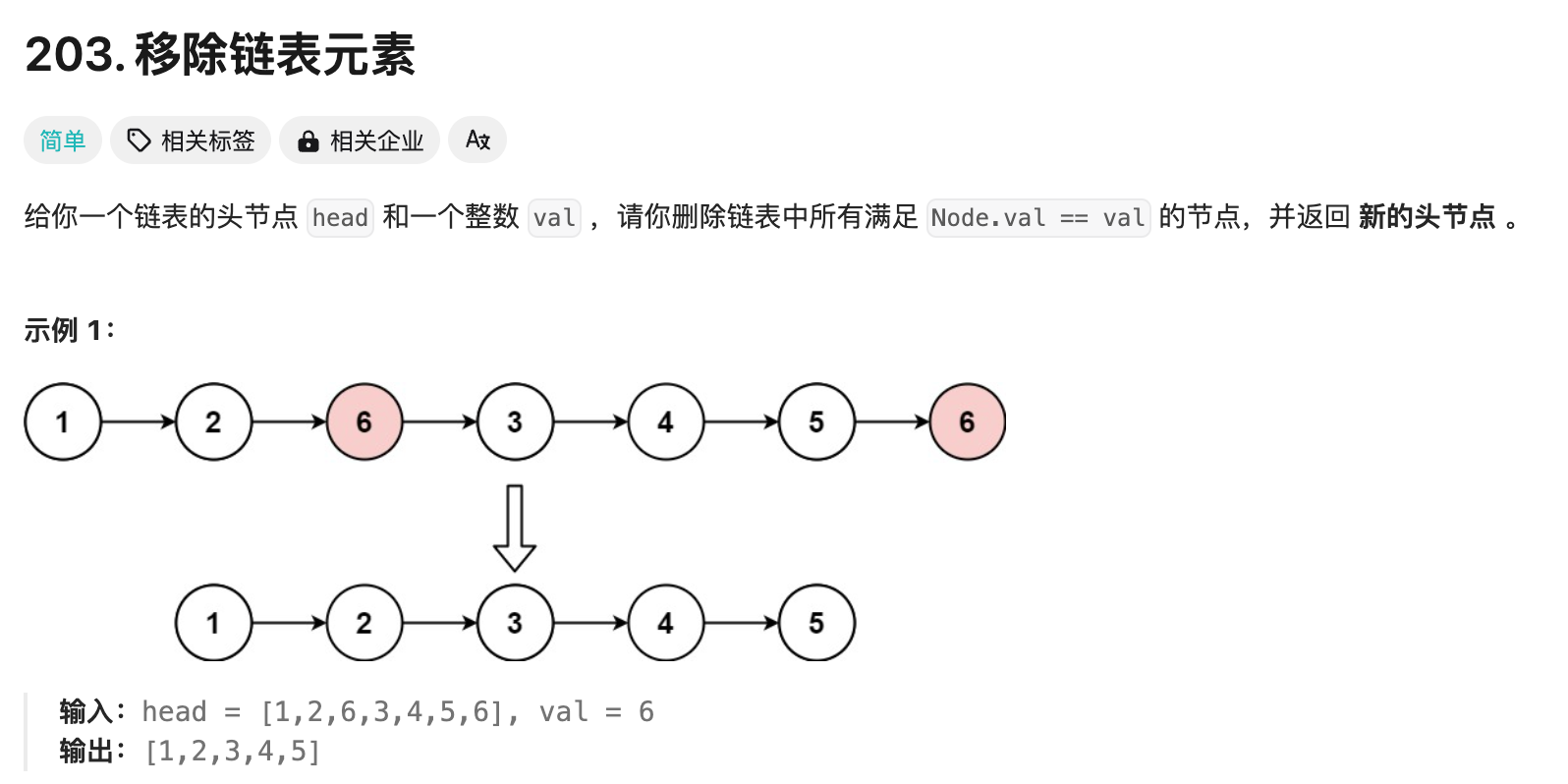
这里就涉及到前面理论部分所讲的链表的删除操作。

但是在实际编写代码过程中可发现：

若直接采用节点 next 指针直接指向下一个节点的方式
则删除头部结点和其他结点的处理是不同的

所以下面我们期望通过一种方式来让两种方式的处理保持一致。

1.1 思路:借助虚拟头结点¶

通过设置一个虚拟头结点，这样原链表的所有节点就都可以按照统一的方式进行移除。

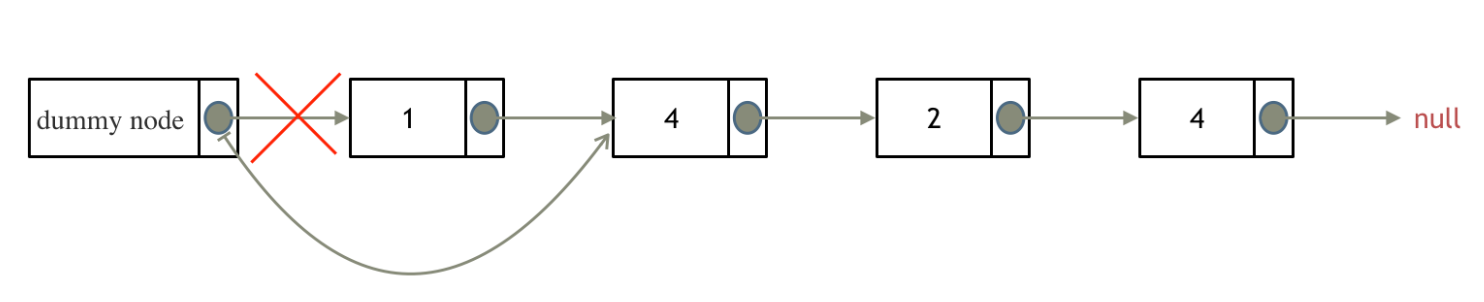
最后在返回头结点的时候，注意需要返回虚拟头结点的 next，具体代码如下：

时间复杂度：\(O(n)\)，空间复杂度:\(O(1)\)

gorust

Go

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func removeElements(head *ListNode, val int) *ListNode {
    dummyHead := &ListNode{}
    dummyHead.Next = head
    cur := dummyHead
    for cur != nil && cur.Next != nil {
        if cur.Next.Val == val {
            cur.Next = cur.Next.Next
        } else {
            cur = cur.Next
        }
    }

    return dummyHead.Next
}

Rust

pub struct Solution;

// Definition for singly-linked list.
#[derive(PartialEq, Eq, Clone, Debug)]
pub struct ListNode {
    pub val: i32,
    pub next: Option<Box<ListNode>>,
}

impl ListNode {
    #[inline]
    fn new(val: i32) -> Self {
        ListNode {
            next: None,
            val,
        }
    }
}

impl Solution {
    pub fn remove_elements(head: Option<Box<ListNode>>, val: i32) -> Option<Box<ListNode>> {
        let mut dummy_head = Box::new(ListNode::new(0));
        dummy_head.next = head;
        let mut cur = dummy_head.as_mut();
        while let Some(nxt) = cur.next.take() {
            if nxt.val == val {
                cur.next = nxt.next;
            } else {
                cur.next = Some(nxt);
                cur = cur.next.as_mut().unwrap();
            }
        }
        dummy_head.next
    }
}

2. 设计链表¶

对应 LeetCode 题目：

该题覆盖了链表所有的基础操作，需要前置掌握链表的理论部分。

2.1 思路:链表基础和哨兵节点¶

结合前面提到的虚拟头结点来完成该题目，具体代码如下：

时间复杂度：涉及 index 的相关操作为 \(O(index)\)，其余为 \(O(1)\)
空间复杂度：\(O(n)\)

gorust

Go

type MyLinkedList struct {
    dummyHead *SingleNode // 虚拟头节点
    Size      int         // 链表大小
}

type SingleNode struct {
    Val  int         // 节点的值
    Next *SingleNode // 下一个节点的指针
}

func NewMyLinkedList() MyLinkedList {
    newNode := &SingleNode{ // 创建新节点
        0,
        nil,
    }
    return MyLinkedList{ // 返回链表
        dummyHead: newNode,
        Size:      0,
    }
}

func (this *MyLinkedList) Get(index int) int {
    if this == nil || index < 0 || index >= this.Size {
        return -1
    }

    cur := this.dummyHead.Next
    for i := 0; i < index; i++ {
        cur = cur.Next
    }
    return cur.Val
}

func (this *MyLinkedList) AddAtHead(val int) {
    newNode := &SingleNode{
        Val:  val,
        Next: this.dummyHead.Next,
    }
    this.dummyHead.Next = newNode
    this.Size++
}

func (this *MyLinkedList) AddAtTail(val int) {
    newNode := &SingleNode{Val: val}
    cur := this.dummyHead
    for cur.Next != nil {
        cur = cur.Next
    }
    cur.Next = newNode
    this.Size++
}

func (this *MyLinkedList) AddAtIndex(index int, val int) {
    if index < 0 {
        index = 0
    } else if index > this.Size {
        return
    }

    newNode := &SingleNode{Val: val}
    cur := this.dummyHead
    for i := 0; i < index; i++ {
        cur = cur.Next
    }
    newNode.Next = cur.Next
    cur.Next = newNode
    this.Size++
}

func (this *MyLinkedList) DeleteAtIndex(index int) {
    if index < 0 || index >= this.Size {
        return
    }
    cur := this.dummyHead
    for i := 0; i < index; i++ {
        cur = cur.Next
    }
    if cur.Next != nil {
        cur.Next = cur.Next.Next
        this.Size--
    }
}

/**
 * Your MyLinkedList object will be instantiated and called as such:
 * obj := Constructor();
 * param_1 := obj.Get(index);
 * obj.AddAtHead(val);
 * obj.AddAtTail(val);
 * obj.AddAtIndex(index,val);
 * obj.DeleteAtIndex(index);
 */

Rust

pub struct Solution;

#[derive(Debug)]
pub struct MyLinkedList {
    pub val: i32,
    pub next: Option<Box<MyLinkedList>>,
}


/**
 * `&self` means the method takes an immutable reference.
 * If you need a mutable reference, change it to `&mut self` instead.
 */
impl MyLinkedList {
    fn new() -> Self {
        MyLinkedList { val: 0, next: None }
    }

    fn get(&self, index: i32) -> i32 {
        if index < 0 {
            return -1;
        }
        let mut i = 0;
        let mut cur = &self.next;
        while let Some(node) = cur {
            if i == index {
                return node.val;
            }
            i += 1;
            cur = &node.next;
        }
        -1
    }

    fn add_at_head(&mut self, val: i32) {
        let new_node = Box::new(MyLinkedList {
            val,
            next: self.next.take(),
        });
        self.next = Some(new_node);
    }

    fn add_at_tail(&mut self, val: i32) {
        let new_node = Box::new(MyLinkedList { val, next: None });
        let mut last_node = &mut self.next;
        while let Some(node) = last_node {
            last_node = &mut node.next;
        }
        *last_node = Some(new_node);
    }

    fn add_at_index(&mut self, index: i32, val: i32) {
        if index <= 0 {
            self.add_at_head(val);
        } else {
            let mut i = 0;
            let mut cur = &mut self.next;
            while let Some(node) = cur {
                if i + 1 == index {
                    let new_node = Box::new(MyLinkedList {
                        val,
                        next: node.next.take(),
                    });
                    node.next = Some(new_node);
                    break;
                }
                i += 1;
                cur = &mut node.next;
            }
        }
    }

    fn delete_at_index(&mut self, index: i32) {
        if index < 0 {
            return;
        }

        let mut i = 0;
        let mut cur = self;
        while let Some(node) = cur.next.take() {
            if i == index {
                cur.next = node.next;
                break;
            }
            i += 1;
            cur.next = Some(node);
            cur = cur.next.as_mut().unwrap();
        }
    }
}

/**
 * Your MyLinkedList object will be instantiated and called as such:
 * let obj = MyLinkedList::new();
 * let ret_1: i32 = obj.get(index);
 * obj.add_at_head(val);
 * obj.add_at_tail(val);
 * obj.add_at_index(index, val);
 * obj.delete_at_index(index);
 */

3. 翻转链表¶

对应 LeetCode 题目：

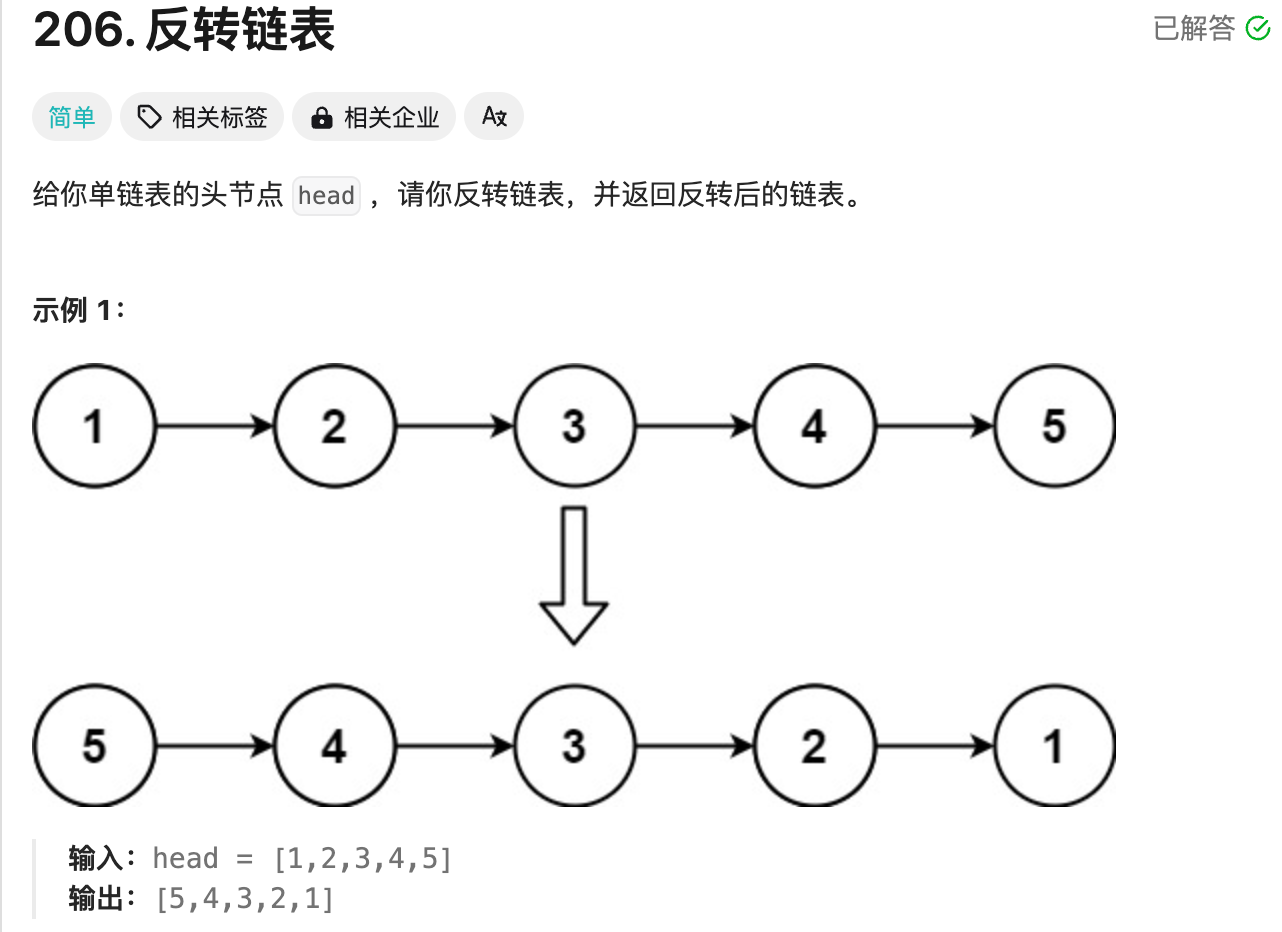
首先我们想到的最简单的解法就是，再定义一个新的链表来实现反转，此解法存在对内存空间浪费，最好可以原地。

3.1 思路:双指针或递归¶

双指针

分别定义 pre 和 cur 两个指针，每次移动 cur 时将 cur->next 指向 pre，最后返回 pre 指针即反转后的头节点。

注意在移动 cur 时，需要使用一个中间指针来暂存 cur 的当前位置，具体代码如下：

时间复杂度：\(O(n)\) ，空间复杂度：\(O(1)\)

gorust

Go

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func reverseList(head *ListNode) *ListNode {
    var cur, pre, tmp *ListNode
    cur = head
    for cur != nil {
        tmp = cur.Next
        cur.Next = pre
        pre = cur
        cur = tmp
    }
    return pre
}

Rust

// Definition for singly-linked list.
#[derive(PartialEq, Eq, Clone, Debug)]
pub struct ListNode {
    pub val: i32,
    pub next: Option<Box<ListNode>>,
}

impl ListNode {
    #[inline]
    fn new(val: i32) -> Self {
        ListNode {
            next: None,
            val,
        }
    }
}

pub struct Solution;


impl Solution {
    pub fn reverse_list(head: Option<Box<ListNode>>) -> Option<Box<ListNode>> {
        let mut pre = None;
        let mut cur = head;
        while let Some(mut node) = cur.take() {
            cur = node.next;
            node.next = pre;
            pre = Some(node);
        }
        pre
    }
}

递归法

递归虽然会抽象一些，但实际上逻辑与双指针一致，核心都是不断移动 cur 后指向 pre，最后在 cur 为空的时候结束。

需要注意的是递归法所需要的空间为 n，具体代码如下：

时间复杂度：\(O(n)\) ，空间复杂度：\(O(n)\)

也存在相反的递归思路，即从后往前翻转指针指向。

gorust

Go

func reverseListOther(head *ListNode) *ListNode {
    var reverse func(*ListNode, *ListNode) *ListNode
    reverse = func(pre *ListNode, cur *ListNode) *ListNode {
        if cur == nil {
            return pre
        }
        temp := cur.Next
        cur.Next = pre
        return reverse(cur, temp)
    }

    return reverse(nil, head)
}

Rust

impl Solution {
    pub fn reverse_list_other(head: Option<Box<ListNode>>) -> Option<Box<ListNode>> {
        fn reverse(mut cur: Option<Box<ListNode>>, mut pre: Option<Box<ListNode>>) -> Option<Box<ListNode>> {
            if let Some(mut node) = cur.take() {
                cur = node.next;
                node.next = pre;
                pre = Some(node);
                return reverse(cur, pre);
            }
            pre
        }
        reverse(head, None)
    }
}

4. 两两交换链表中的节点¶

对应 LeetCode 题目：

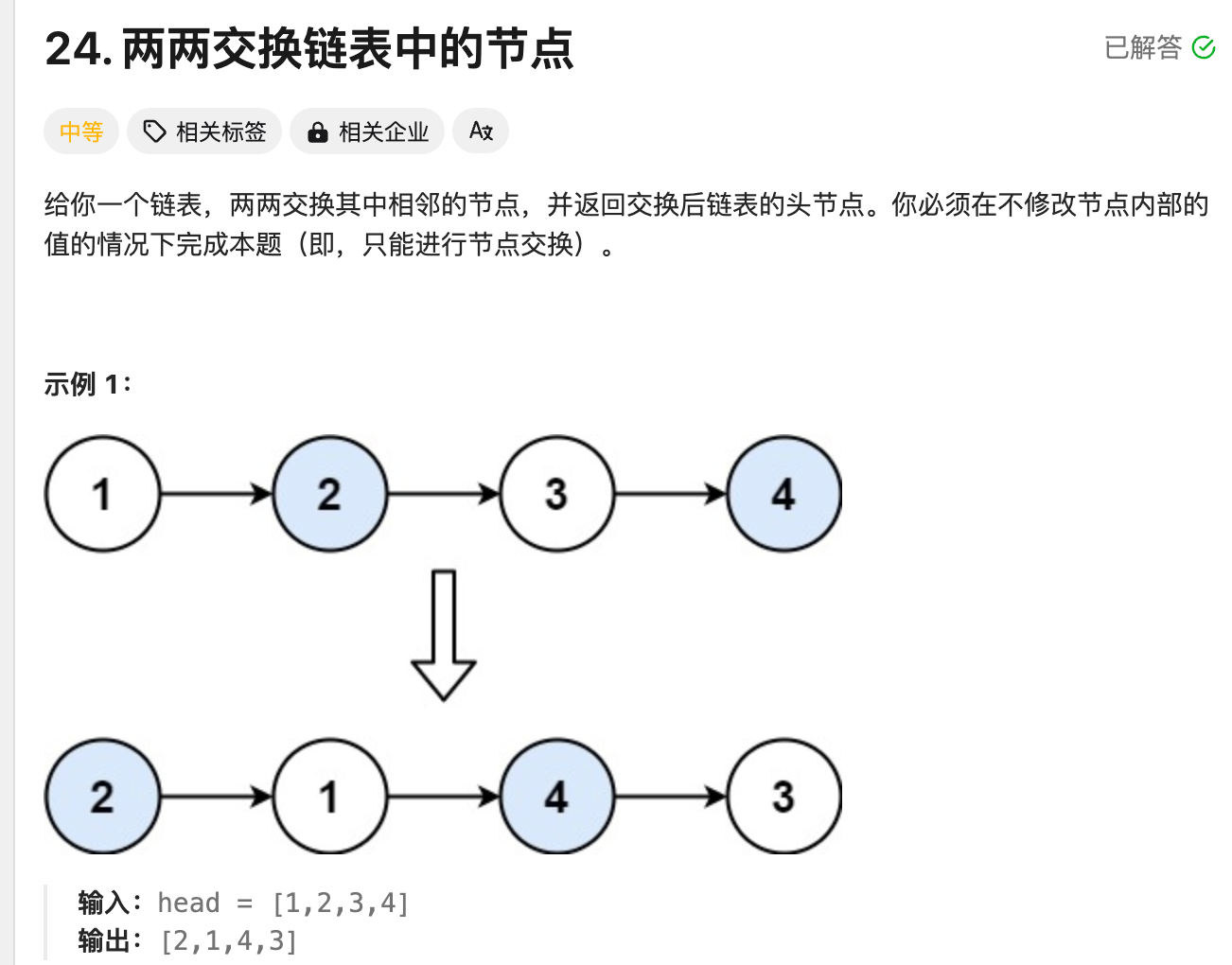
此题正常模拟，主要考查链表的操作，可使用画图来清晰表示。

4.1 思路:虚拟头节点或递归¶

交换的步骤如下图示：

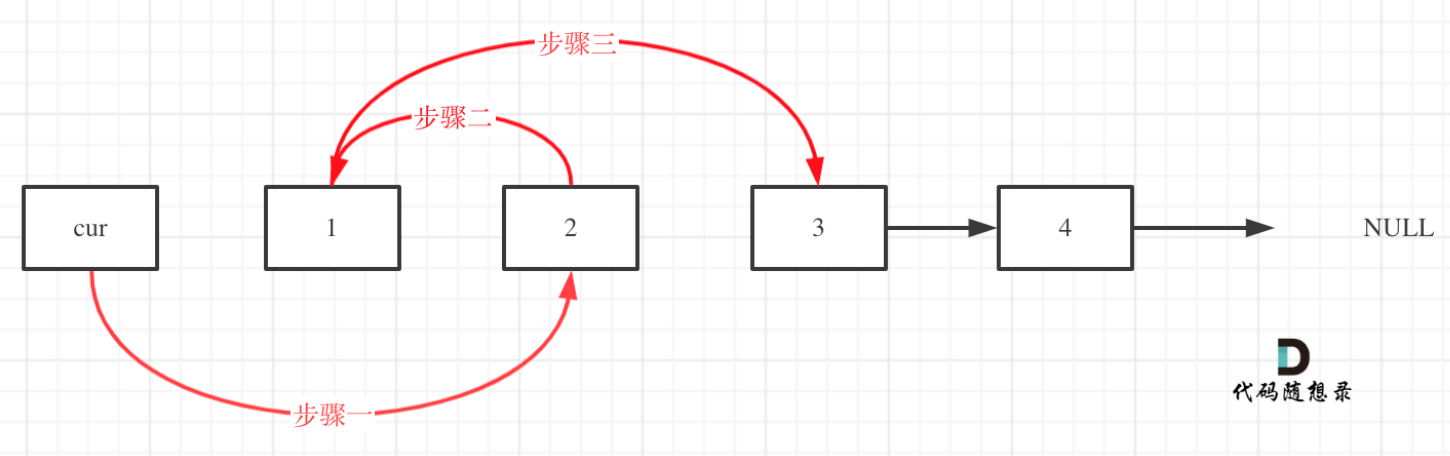
虚拟头节点和递归的解法按照上面步骤，具体代码如下：

时间复杂度：\(O(n)\) ，空间复杂度：\(O(1)\)

gorust

Go

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func swapPairs(head *ListNode) *ListNode {
    if head == nil || head.Next == nil {
        return head
    }
    dummyHead := &ListNode{0, nil}
    dummyHead.Next = head
    cur := dummyHead
    for cur.Next != nil && cur.Next.Next != nil {
        tmp := cur.Next
        tmp1 := cur.Next.Next.Next

        cur.Next = cur.Next.Next
        cur.Next.Next = tmp
        cur.Next.Next.Next = tmp1

        cur = cur.Next.Next
    }
    return dummyHead.Next
}

func swapPairsOther(head *ListNode) *ListNode {
    if head == nil || head.Next == nil {
        return head
    }
    next := head.Next
    head.Next = swapPairsOther(next.Next)
    next.Next = head
    return next
}

Rust

// Definition for singly-linked list.
#[derive(PartialEq, Eq, Clone, Debug)]
pub struct ListNode {
    pub val: i32,
    pub next: Option<Box<ListNode>>,
}

impl ListNode {
    #[inline]
    fn new(val: i32) -> Self {
        ListNode {
            next: None,
            val,
        }
    }
}

pub struct Solution;

impl Solution {
    pub fn swap_pairs(head: Option<Box<ListNode>>) -> Option<Box<ListNode>> {
        let mut dummy_head = Box::new(ListNode::new(0));
        dummy_head.next = head;
        let mut cur = dummy_head.as_mut();
        while let Some(mut node) = cur.next.take() {
            if let Some(mut next) = node.next.take() {
                node.next = next.next.take();
                next.next = Some(node);
                cur.next = Some(next);
                cur = cur.next.as_mut().unwrap().next.as_mut().unwrap();
            } else {
                cur.next = Some(node);
                cur = cur.next.as_mut().unwrap();
            }
        }
        dummy_head.next
    }
}