数组算法¶

1. 二分查找¶

核心点

有序数组
将目标值与数组中间元素进行比较，从而排除掉一半的元素，如此循环，直到找到目标值或确定目标值不存在
通常时间复杂度：\(O(logn)\)

其中需要注意:

区间范围决定了边界（包含起始位置）的值，可通过构造简单的有序数组来演算进行理解

1.1 算法:二分法¶

代码模版(点击展开)

左闭右闭 [left, right]左闭右开 [left, right)

Go

func search(nums []int, target int) int {
    high := len(nums)-1
    low := 0
    for low <= high {
        mid := low + (high-low)/2
        if nums[mid] == target {
            return mid
        } else if nums[mid] > target {
            high = mid-1
        } else {
            low = mid+1
        }
    }
    return -1
}

Go

func search(nums []int, target int) int {
    left, right := 0, len(nums)
    for left < right {
        mid := left + (right-left)/2
        if nums[mid] > target {
            right = mid
        } else if nums[mid] < target {
            left = mid + 1
        } else {
            return mid
        }
    }

    return -1
}

1.2 相关题目¶

704二分查找
35.搜索插入位置
34.在排序数组中查找元素的第一个和最后一个位置
69.x 的平方根
367.有效的完全平方数

2. 移除元素¶

对应 LeetCode 题目：

Note

数组的元素在内存地址中是连续的，不能单独删除数组中的某个元素，只能覆盖。

若采取暴力解法，则类似于冒泡排序进行两层遍历，下面重点说明双指针法。

2.1 算法:双指针法¶

双指针法（快慢指针法）：

通过一个快指针和慢指针在一个for循环下完成两个for循环的工作

定义快慢指针：

快指针：寻找新数组的元素，新数组就是不含有目标元素的数组
慢指针：指向更新新数组下标的位置

此思路不仅应用在数组中，在其他如链表、字符串等都有相应应用。

下面两个解法均可满足题意，后者的优点在于确保移动的最小次数

时间复杂度：\(O(n)\)
空间复杂度：\(O(1)\)

解法一解法二

Go

func removeElement(nums []int, val int) int {
    slow := 0
    for fast := 0; fast < len(nums); fast++ {
        if val != nums[fast] {
            nums[slow] = nums[fast]
            slow++
        }
    }
    return slow
}

Go

func removeElement(nums []int, val int) int {
    leftIdx, rightIdx := 0, len(nums)-1
    for leftIdx <= rightIdx {

        for leftIdx <= rightIdx && nums[leftIdx] != val {
            leftIdx++
        }

        for leftIdx <= rightIdx && nums[rightIdx] == val {
            rightIdx--
        }

        if leftIdx < rightIdx {
            nums[leftIdx] = nums[rightIdx]
            leftIdx++
            rightIdx--
        }
    }

    return leftIdx
}

2.2 相关题目¶

3.长度最小的子数组¶

对应 LeetCode 题目：

Note

涉及到连续子数组的处理，可考虑使用滑动窗口的算法思想来解决

若采取暴力解法，则是通过两层循环不断寻找符合条件的子序列，下面重点说明滑动窗口解法。

3.1 算法:滑动窗口¶

滑动窗口的主要思想：

不断的调节子序列的起始位置和终止位置，从而得出预期结果

滑动窗口的实现通常需要确认如下三点：

窗口内是什么？
- 满足其和≥s的长度最小的连续子数组
如何移动窗口的起始位置？
- 若当前窗口的值大于s则窗口需要向前移动了
如何移动窗口的结束位置？
- 窗口的结束位置就是遍历数组的指针

具体实现代码如下：时间复杂度：\(O(n)\) ，空间复杂度：\(O(1)\)

Go

func minSubArrayLen(target int, nums []int) int {
    start, end := 0, 0
    result := len(nums) + 1
    cur := 0
    for ; end < len(nums); end++ {
        cur += nums[end]
        for ; cur >= target; start++ {
            result = min(result, end-start+1)
            cur -= nums[start]
        }
    }

    if result == len(nums)+1 {
        return 0
    }
    return result
}

3.2 相关题目¶

209.长度最小的子数组
904.水果成篮
76.最小覆盖子串

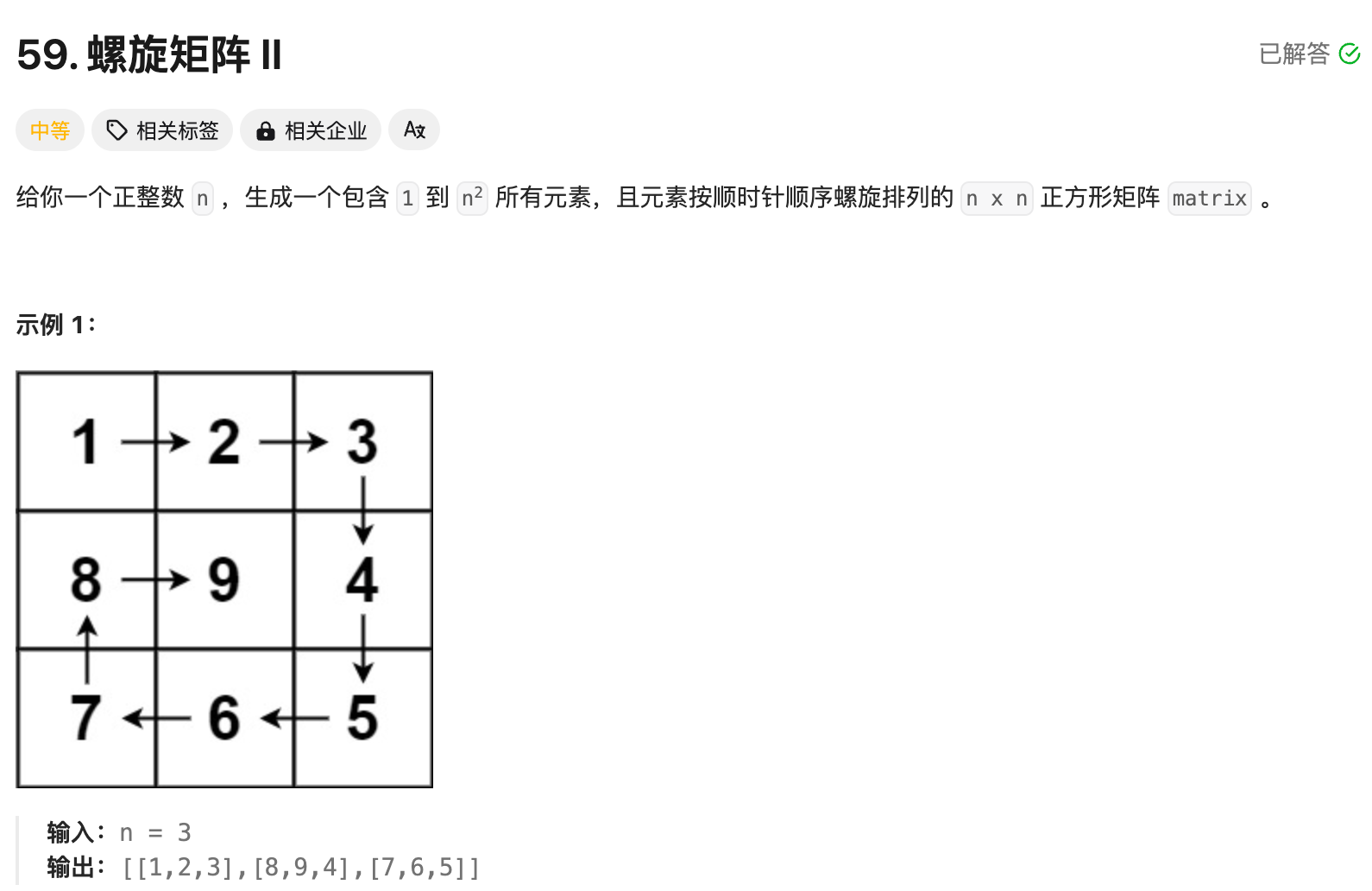
4. 螺旋矩阵II¶

对应 LeetCode 题目：

Note

此题重要的不是算法，而是考察模拟的过程

4.1 算法:模拟过程¶

在上面提到二分法的时候就提到，如果要写出正确的二分法一定要坚持循环不变量原则。

而求解此题依然是要坚持循环不变量原则，模拟顺时针画矩阵的过程:

填充上行从左到右
填充右列从上到下
填充下行从右到左
填充左列从下到上

这里我们就需要保持循环不变量，保持每条边左闭右开的原则，具体代码如下：

时间复杂度：\(O(n^2)\)，空间复杂度：\(O(1)\)

gorust

Go

func generateMatrix(n int) [][]int {
        result := make([][]int, n)
        for i, _ := range result {
                result[i] = make([]int, n)
        }
        startX, startY := 0, 0
        mid := n / 2
        count, offset := 1, 1
        for loop := n / 2; loop > 0; loop-- {
                i, j := startX, startY

                for j = startY; j < n-offset; j++ {
                        result[startX][j] = count
                        count++
                }
                for i = startX; i < n-offset; i++ {
                        result[i][j] = count
                        count++
                }
                for ; j > startY; j-- {
                        result[i][j] = count
                        count++
                }
                for ; i > startX; i-- {
                        result[i][j] = count
                        count++
                }

                startX++
                startY++
                offset++
        }

        if n%2 > 0 {
                result[mid][mid] = count
        }
        return result
}

Rust

impl Solution {
    pub fn generate_matrix(n: i32) -> Vec<Vec<i32>> {
        let mut result = vec![vec![0; n as usize]; n as usize];
        let (mut start_x, mut start_y) = (0, 0);
        let mid = (n / 2) as usize;
        let (mut offset, mut count) = (1, 1);
        for _ in (0..(n / 2)).rev() {
            let (mut i, mut j) = (start_x, start_y);

            for _ in start_y..(n as usize - offset) {
                result[start_x][j] = count;
                count += 1;
                j += 1;
            }

            for _ in start_x..(n as usize - offset) {
                result[i][j] = count;
                count += 1;
                i += 1;
            }

            for _ in 0..(j - start_y) {
                result[i][j] = count;
                count += 1;
                j -= 1;
            }

            for _ in 0..(i - start_x) {
                result[i][j] = count;
                count += 1;
                i -= 1;
            }

            start_x += 1;
            start_y += 1;
            offset += 1;
        }

        if n % 2 > 0 {
            result[mid][mid] = count;
        }
        result
    }
}

4.2 相关题目¶

54.螺旋矩阵
59.螺旋矩阵II
剑指Offer29.顺时针打印矩阵